
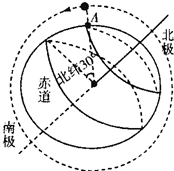
 �������ǵ����й��ƽ��ͨ��������ϱ��������������ΪԲ���������ͼ��ʾ����ij�������Ǵӱ�γ30��A������Ϸ���ͼʾ�����һ����������γ30�����Ϸ�������ʱ��Ϊt����֪����뾶ΪR������ɿ������壩�����������������ٶ�Ϊg����������ΪG��������������֪��������
�������ǵ����й��ƽ��ͨ��������ϱ��������������ΪԲ���������ͼ��ʾ����ij�������Ǵӱ�γ30��A������Ϸ���ͼʾ�����һ����������γ30�����Ϸ�������ʱ��Ϊt����֪����뾶ΪR������ɿ������壩�����������������ٶ�Ϊg����������ΪG��������������֪��������| A�� | ���Ǵ�ͼʾλ���پ���ʱ��6tһ���ֻص�A������Ϸ� | |
| B�� | ���Ǵ�ͼʾλ���پ���ʱ��6.5tһ����������������Ϸ� | |
| C�� | �������е����ٶ�Ϊ$\frac{��R}{3t}$ | |
| D�� | ���Ǿ����ĸ߶ȣ�$\frac{9g{R}^{2}{t}^{2}}{{��}^{2}}$��${\;}^{\frac{1}{3}}$ |
���� ����������Բ���˶�����ϼ��ι�ϵ������ǵ������Լ��˶���������Ϸ������ʱ�䣮�������������ṩ��������������������������������ڵĴ�С������Ǿ������ĸ߶ȣ�ע�����ǵĹ���뾶�����ڵ���İ뾶��
��� �⣺A���������Ǵӱ�γ30��A������Ϸ���ͼʾ�����һ����������γ30�����Ϸ���ת���ĽǶ�Ϊ60�㣬��ת��һȦ��Ҫ����6t�����ǵ�������ת����һ����A�����Ϸ�����A����
B����A�㵽��һ�ε�����Ϸ�ת���ĽǶ�Ϊ30�㣬�����ʱ��Ϊ0.5t����֪����6.5t��������������Ϸ�����B��ȷ��
C���������ǵĹ���뾶����R�������ٶ�v��$\frac{\frac{1}{6}��2��R}{t}=\frac{��R}{3t}$����C����
D��������֪�����ǵ�����T=6t������$G\frac{Mm}{��R+h��^{2}}=m��R+h��\frac{4{��}^{2}}{{T}^{2}}$��GM=gR2�ã��������h=$\root{3}{\frac{9g{R}^{2}{t}^{2}}{{��}^{2}}}-R$����D����
��ѡ��B��
���� �������Ĺؼ����������������ɵ�������Ҫ���ۣ�1��������������������2�����������ṩ������������������ã�


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
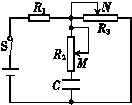
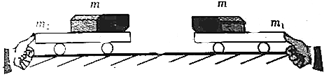
| A�� | ����ƬN���һ���ʱ��R2�������ϵĵ��� | |
| B�� | ����ƬN���һ���ʱ��R2�������µĵ��� | |
| C�� | ����ƬM���ϻ���ʱ��R2�������ϵĵ��� | |
| D�� | ����ƬM���ϻ���ʱ��R2�������µĵ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������������������ǵ����������ȣ�������֮��ľ���ɷ��� | |
| B�� | �����ϵ�����͵����������ܵ����������ǵ����������������� | |
| C�� | ����������������������������������������� | |
| D�� | �κ��������嶼��������ģ������Ĵ�С�����ǵ������ij˻������ȣ������ǵľ����ƽ���ɷ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
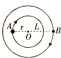 ��ͼ��ʾΪ����ϵ��A��B���ź�����ɵ�˫��ϵͳ����֪AB��ľ���ΪL�������A������AB������O����Բ���˶�������ΪT������뾶Ϊr���������ǵ�����Ϊ����������ΪG����������
��ͼ��ʾΪ����ϵ��A��B���ź�����ɵ�˫��ϵͳ����֪AB��ľ���ΪL�������A������AB������O����Բ���˶�������ΪT������뾶Ϊr���������ǵ�����Ϊ����������ΪG����������| A�� | mA=$\frac{4{��}^{2}��L-r��{L}^{2}}{G{T}^{2}}$ | B�� | mB=$\frac{4{��}^{2}r{L}^{2}}{G{T}^{2}}$ | ||
| C�� | mA=$\frac{4{��}^{2}��L-r��^{3}}{G{T}^{2}}$ | D�� | mB=$\frac{4{��}^{2}{r}^{3}}{G{T}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
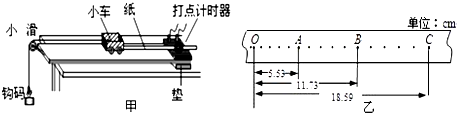
| ���ģ����ţ� | ��� |
| ������A1 ������A2 ��ѹ��V1 ���裨R1�� �����䣨R2�� ������������R3�� ������������R4�� ��Դ��E1�� ��Դ��E2�� ���أ�S1�� ���أ�S2�� �������� | ����10mA������r1Լ��Լ40���� ����300��A������r2=750�� ����10V������r3=10K�� ��ֵԼΪ120������������ ��ֵ��Χ0��3900�� ����ֵԼ50�� ����ֵԼ1k�� �綯��1.5V�������С �綯��6V�������С |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
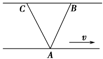 ��ͼ��ʾΪһ����������ˮ����Ϊv��һֻ����A���Ⱥ����ζɺӵ��������ھ�ˮ����ʻ���ٶ�Ϊu����һ�δ�ͷ����AB������ʻ���ɺ�ʱ��Ϊt1������λ��Ϊs1���ڶ��δ�ͷ����AC������ʻ���ɺ�ʱ��Ϊt2������λ��Ϊs2����AB��AC��Ӱ��Ĵ��߷���ļн���ȣ����У�������
��ͼ��ʾΪһ����������ˮ����Ϊv��һֻ����A���Ⱥ����ζɺӵ��������ھ�ˮ����ʻ���ٶ�Ϊu����һ�δ�ͷ����AB������ʻ���ɺ�ʱ��Ϊt1������λ��Ϊs1���ڶ��δ�ͷ����AC������ʻ���ɺ�ʱ��Ϊt2������λ��Ϊs2����AB��AC��Ӱ��Ĵ��߷���ļн���ȣ����У�������| A�� | t1=t2 | B�� | t1��t2 | C�� | s1��s2 | D�� | s1��s2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com