

���� �ٸ���ʵ���ԭ���Լ������е�ע������ȷ����ȷ�IJ������裮
�ڸ����������ʱ���ڵ�λ��֮����һ���������������С���˶��ļ��ٶȣ�
�۸������ڵIJ�������ϡ�x=aT2ȷ�����ٶȵIJ�����
��� �⣺��A��̽��С���ȱ���ֱ���˶��Ĺ��ɣ�ľ���Ƿ�⻬��ʵ��û��Ӱ�죬��A����
B��Ϊ�˱��ڲ�����ʹ�õ㼣��ľ����ʵ���һЩ��ѡ��������һЩ������Ͱ����B����
C��ʵ��ʱ��С��Ӧ�����ܿ�������ʱ������C��ȷ��
D��ϸ��Ӧ������ľ��ƽ�У���D��ȷ��
��ѡ��CD��
�ڸ��ݡ�x=aT2���������ã�a=$\frac{{x}_{CE}-{x}_{AC}}{4{T}^{2}}=\frac{��8.21+9.69-6.20-7.70����1{0}^{-2}}{4��0.01}$=1.0m/s2��
����ʵ���в��õĽ�����Ƶ�ʵ���50Hz�������ڵIJ���ֵ��ʵ��ֵƫС������$a=\frac{��x}{{T}^{2}}$֪�����ٶȵIJ���ֵƫ��
�ʴ�Ϊ����CD����1.0����ƫ��
���� �������Ĺؼ�֪��ʵ���ԭ���Լ������е�ע���������ֽ���Ĵ�����������ͨ��ֽ�����˲ʱ�ٶȺͼ��ٶȣ�


 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ�����˻�Խ��Խ�ܵ����Ƽ��ԵĻ�ӭ������������������λȷ���ص㣬�������ں��ģ����ģ���ݣ�Ұ���۲�ȵ�����森ij�λ�У�����Ա��Ҫ����ͣ��H=300m�߿յ�����Ϊm=2kg���˻���ȫ��ֱ�½�����أ������ȹرն���ϵͳ�����˻������ٶ�Ϊ�����ֱ�ȼ���ֱ���˶����½�t1=5sʱ��������ϵͳ�������˻��ṩ�㶨����ֱ���ϵ�����F��ʹ�����ȼ���ֱ���˶������½�t2=25s�ٶ�ǡ�ü�Ϊ��ʱ��½�������˻��½��������ܵ������������㶨�������ĸ����ɺ��Բ��ƣ�ȡg=10m/s2����
��ͼ�����˻�Խ��Խ�ܵ����Ƽ��ԵĻ�ӭ������������������λȷ���ص㣬�������ں��ģ����ģ���ݣ�Ұ���۲�ȵ�����森ij�λ�У�����Ա��Ҫ����ͣ��H=300m�߿յ�����Ϊm=2kg���˻���ȫ��ֱ�½�����أ������ȹرն���ϵͳ�����˻������ٶ�Ϊ�����ֱ�ȼ���ֱ���˶����½�t1=5sʱ��������ϵͳ�������˻��ṩ�㶨����ֱ���ϵ�����F��ʹ�����ȼ���ֱ���˶������½�t2=25s�ٶ�ǡ�ü�Ϊ��ʱ��½�������˻��½��������ܵ������������㶨�������ĸ����ɺ��Բ��ƣ�ȡg=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
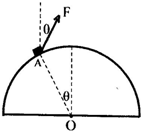 ��ͼ����ij�ֲ����ƳɵĹ̶���ˮƽ�����ϰ�Բ����Ľ���ͼ��O��ΪԲ�ģ���Բ��������ǹ⻬�ģ�����Ϊm��С��飨��Ϊ�ʵ㣩������ֱ�����30��ǵ�б���ϵ�����F�����¾�ֹ��A�����뾶OA����ֱ����ļн�ҲΪ30�㣮��O��F����ͬһ������ڣ���С����Բ��������ѹ��Ϊ��������
��ͼ����ij�ֲ����ƳɵĹ̶���ˮƽ�����ϰ�Բ����Ľ���ͼ��O��ΪԲ�ģ���Բ��������ǹ⻬�ģ�����Ϊm��С��飨��Ϊ�ʵ㣩������ֱ�����30��ǵ�б���ϵ�����F�����¾�ֹ��A�����뾶OA����ֱ����ļн�ҲΪ30�㣮��O��F����ͬһ������ڣ���С����Բ��������ѹ��Ϊ��������| A�� | $\frac{\sqrt{3}}{3}$mg | B�� | mg | C�� | $\sqrt{3}$mg | D�� | $\frac{1}{2}$mg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
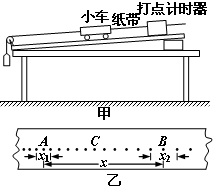 ijʵ��С�������ͼ����ʾ��װ��̽��С���� б���ϵ��˶������ʵ��������ͨ����������ֵ�ϸ������С����С���ִ���ֽ�����ȱ���ֱ���˶���ͨ������ʱ����ֽ���ϴ���һϵ�е㣨��ͼ����ʾ���������Ŵ���ʱ���������ΪT�����ͼ�е���Ӧ����֮��ľ���x��x1��x2����
ijʵ��С�������ͼ����ʾ��װ��̽��С���� б���ϵ��˶������ʵ��������ͨ����������ֵ�ϸ������С����С���ִ���ֽ�����ȱ���ֱ���˶���ͨ������ʱ����ֽ���ϴ���һϵ�е㣨��ͼ����ʾ���������Ŵ���ʱ���������ΪT�����ͼ�е���Ӧ����֮��ľ���x��x1��x2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | һ����������ѹǿ�����¶�����ʱ�����յ�����һ���������ܵ����� | |
| B�� | �����ø߿Ƽ��ֶΣ�����ɢ������ȫ���ռ��������ã��������������仯 | |
| C�� | �߿��еı����ڿ��������������ʱ������������ | |
| D�� | �����Ӽ���������Ϊ����ʱ������Ӽ�û�г��� | |
| E�� | �����˶������Ƿ��ӵ������˶�����Һ����������˶��ķ�ӳ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
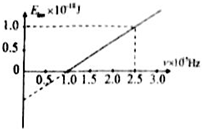 ��ij��ɫ����������ѱ��棬�������ЧӦ�����ѱ���ų�����ӵ����������������Ƶ�ʵĹ�ϵͼ����ͼ����֪���ʿ˳���Ϊ6.67��10-34J•s��������˵����ȷ���ǣ�������
��ij��ɫ����������ѱ��棬�������ЧӦ�����ѱ���ų�����ӵ����������������Ƶ�ʵĹ�ϵͼ����ͼ����֪���ʿ˳���Ϊ6.67��10-34J•s��������˵����ȷ���ǣ�������| A�� | �ѵ��ݳ���Ϊ6.67��10-19J | |
| B�� | �ѵļ���Ƶ��Ϊ1.0��1015Hz | |
| C�� | ����ӵ���������Ϊ1.0��10-18J | |
| D�� | �ò�ͬƵ�ʵĵ�ɫ����������ѱ��棬�����ܷ������ЧӦ�������������ܲ�����ͬ | |
| E�� | ����ӵ�����������������Ƶ�ʳ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
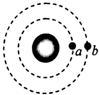
| A�� | a��b���ٶ�֮��Ϊ3��2 | B�� | a��b���ٶ�֮��Ϊ2$\sqrt{2}$��3$\sqrt{3}$ | ||
| C�� | a��b����֮��Ϊ2$\sqrt{2}$��3$\sqrt{3}$ | D�� | a��b���ļ��ٶ�֮��Ϊ4��9 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | $\frac{s}{{v}_{0}}$ | B�� | $\sqrt{\frac{2h}{g}}$ | C�� | $\frac{{v}_{1}}{g}$ | D�� | $\frac{\sqrt{{{v}_{1}}^{2}-{{v}_{0}}^{2}}}{g}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com