
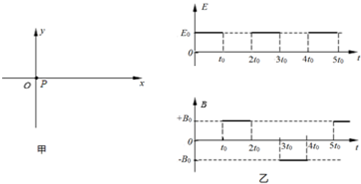
分析 (1)0.5t0时刻释放的粒子先在电场中经过0.5t0时间的加速,再进入磁场,进入磁场的速度就是在电场中加速的末速度.
(2)t0-2t0粒子在磁场中做匀速圆周运动,只有当t=2t0时刻粒子的速度方向沿x轴负向,粒子才能做往复运动,画出运动轨迹,粒子在磁场中运动3/2个圆周再加上电场中的轨迹和长度,就是粒子第一次回到出发点所通过的路程.
(3)粒子交替在电场和磁场中加速、圆周运动、减速为零到达y轴,再加速、圆周运动、减速为零到达y轴,如此循环,显然在y轴的纵坐标有一定的规律,找出第一次、第二次纵坐标的规律,就能写出一般规律.
解答 解:(1)0.5t0-t0粒子在电场中做匀加速直线运动,
电场力F=E0q
加速度 a=$\frac{F}{q}$
速度 v0=at t=0.5t0
解得:v0=$\frac{{E}_{0}q{t}_{0}}{2m}$
(2)t0-2t0粒子在磁场中做匀速圆周运动,只有当t=2t0时刻粒子的速度方向沿x轴负向,粒子才能做
往复运动.${B}_{0}q{v}_{0}=\frac{m{{v}_{0}}^{2}}{R}$ $T=\frac{2πR}{{v}_{0}}$ 由以上两式解得:$T=\frac{2}{3}{t}_{0}$ 由此判断出粒子在磁场中运动
3/2个圆周,粒子轨迹如图所示,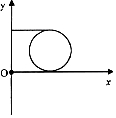
粒子第一次回到出发点通过的路程S=S磁+S电
粒子在磁场中通过的路程 S磁=3v0T=$\frac{{E}_{0}q{t}^{2}}{m}$
粒子在电场中路程 ${S}_{电}=4×\frac{0+{v}_{0}}{2}×\frac{1}{2}{t}_{0}$=$\frac{{E}_{0}q{{t}_{0}}^{2}}{2m}$
所以 S=$\frac{3{E}_{0}q{{t}_{0}}^{2}}{2m}$
(3)t′时刻释放粒子,在电场中加速时间为t0-t′,进入磁场中的速度:
v1=a(t0-t′)═
进入磁场后做圆周运动,由${B}_{0}q{v}_{1}=m\frac{{{v}_{1}}^{2}}{{r}_{1}}$,可得${r}_{1}=\frac{m{v}_{1}}{{B}_{0}q}=\frac{{E}_{0}({t}_{0}-t′)}{{B}_{0}}$
2t0时刻开始在电场中运动,经(t0-t′)时间速度减为零,粒子到达y轴,而后粒子在电场中再次向右
加速t′时间,再次进入磁场中的速度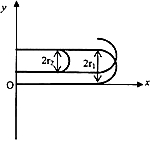
${v}_{2}=at′=\frac{{E}_{0}qt′}{m}$ 由 $q{v}_{2}B=m\frac{{{v}_{2}}^{2}}{{r}_{2}}$ 可得 ${r}_{2}=\frac{m{v}_{2}}{q{B}_{0}}=\frac{{E}_{0}t′}{{B}_{0}}$
上述 r1>r2 粒子运行轨迹如图所示
综上分析,速度为零时粒子横坐标为x=0
纵坐标为
$y=\left\{\begin{array}{l}{2[k{r}_{1}-(k-1){r}_{2}]}\\{2k({r}_{1}-{r}_{2})}\end{array}\right.\\;\\;(k=1,2,3,4…)$ (k=1,2,3,4…)
即$y=\left\{\begin{array}{l}{\frac{2{E}_{0}[k({t}_{0}-2t′)+{t}_{0}]}{{B}_{0}}}\\{\frac{2k{E}_{0}({t}_{0}-2t′)}{{B}_{0}}}\end{array}\right.$ (k=1,2,3,4…)
答:(1)P在磁场中运动时速度的大小为$\frac{{E}_{0}q{t}_{0}}{2m}$.
(2)若B0=$\frac{3πm}{q{t}_{0}}$,求粒子第一次回到出发点所通过的路程是$\frac{3{E}_{0}q{{t}_{0}}^{2}}{2m}$.
(3)若在t′(0<t′<0.5t0)时刻释放P,粒子P速度为零时的横坐标为x=0,纵坐标为$y=\left\{\begin{array}{l}{\frac{2{E}_{0}[k({t}_{0}-2t′)+{t}_{0}]}{{B}_{0}}}\\{\frac{2k{E}_{0}({t}_{0}-2t′)}{{B}_{0}}}\end{array}\right.$ (k=1,2,3,4…).
点评 本题的关键是:①题干中所限制的粒子P必须能做往返运动,那样粒子做圆周运动的周期与交变磁场的周期有一定的关系.②第三问涉及的多解问题,加速时间小于0.5t0,则第一次加速时间较长,速度大,进入磁场后做匀速圆周运动的半径也大,返回时刚好到y轴速度为零,而第二次加速时间短,进入磁场的速度小,半径小,所以再次到达y轴的坐标就变小,余次类推找出一般规律即可.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:填空题
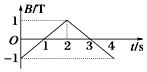 一个边长为10cm的正方形金属线框置于匀强磁场中,线框匝数n=100,线框平面与磁场垂直,电阻为20Ω.磁感应强度随时间变化的图象如图所示.则前两秒产生的电动势为1 V.
一个边长为10cm的正方形金属线框置于匀强磁场中,线框匝数n=100,线框平面与磁场垂直,电阻为20Ω.磁感应强度随时间变化的图象如图所示.则前两秒产生的电动势为1 V.查看答案和解析>>
科目:高中物理 来源:2017届安徽师范大学附中高三上学期期中考试物理试卷(解析版) 题型:实验题
如图1所示,将打点计时器固定在铁架台上,用重物带动纸带从静止开始自由下落,利用此装置可验证机械能守恒定律.
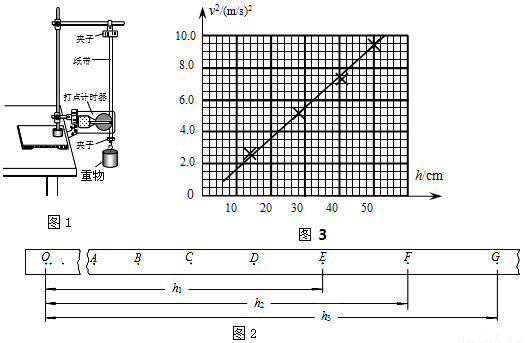
①已准备的器材有打点计时器(带导线)、纸带、复写纸、带铁夹的铁架台和带夹子的重物,此外还需要的器材是__________(填字母代号).
A.直流电源、天平及砝码
B.直流电源、毫米刻度尺
C.交流电源.天平及砝码
D.交流电源、毫米刻度尺
②实验中需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h.某同学对实验得到的纸带,设计了以下四种测量方案,这些方案中合理的是:__________.
A.用刻度尺测出物体下落的高度h,由打点间隔数算出下落时间t,通过v=gt计算出瞬时速度v
B.用刻度尺测出物体下落的高度h,并通过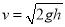 计算出瞬时速度v
计算出瞬时速度v
C.报据做匀变速直线运动时,纸带上某点的瞬时速度等于这点前后相邻两点间的平均速度,测算出瞬时速度v,并通过计算得出高度h
D.用刻度尺测出物体下落的高度h,根据做匀变速直线运动时,纸带上某点的瞬时速度等于这点前后相邻两点间的平均速度,测算出瞬时速度v
③安装好实验装置,正确进行实验操作,从打出的纸带中选出符合要求的纸带,如图2所示.图中O点为打点起始点,且速度为零.选取纸带上打出的连续点A、B、C、…作为计数点,测出其中E、F、G点距起始点O的距离分別为h1、h2、h3.已知重锤质量为m,当地重力加速度为g,计时器打点周期为T.为了验证此实验过程中机械能是否守恒,需要计算出从O点到F点的过程中,重锤重力势能的减少量△Ep=__________,动能的增加量△Ek=__________(用题中所给字母表示)
④实验结果往往是重力势能的减少量略大于动能的增加量,关于这个误差下列说法正确的是__________.
A.该误差属于偶然误差
B.该误差属于系统误差
C.可以通过多次测量取平均值的方法来减小该误差
D.可以通过减小空气阻力和摩擦阻力的影响来减小该误差
⑤某同学在实验中发现重锤增加的动能略小于重锤减少的重力势能,于是深入研究阻力对本实验的影响.若重锤所受阻力为f.重锤质量为m,重力加速度为g.他测出各计数点到起始点的距离h,并计算出各计数点的速度v,用实验测得的数据绘制出v2﹣h图线,如图3所示,图象是一条直线,此直线斜率k=__________(用题中字母表示).
已知当地的重力加速度g=9.8m/s2,由图线求得重锤下落时受到阻力与重锤所受重力的百分比为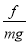 =__________% (保留两位有效数字).
=__________% (保留两位有效数字).
查看答案和解析>>
科目:高中物理 来源:2016-2017学年山东省高二上学期期中考物理试卷(解析版) 题型:实验题
在“测定金属丝的电阻率”的实验中,待测电阻丝阻值约为4Ω。
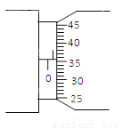
(1)用螺旋测微器测量电阻丝的直径d。其中一次测量结果如图所示,图中读数为d= mm。
(2)为了测量电阻丝的电阻R,除了导线和开关外,还有以下一些器材可供选择:
电压表V;量程3V,内阻约为3kΩ
电流表A1;量程0.6A,内阻约为0.2Ω)
电流表A2;量程100μA,内阻约为2000Ω)
滑动变阻器R1, 阻值0~1750Ω,额定电流为0.3A
滑动变阻器R2,阻值0~50Ω,额定电流为1A
电源E1(电动势15V,内阻约为0.5Ω)
电源E2(电动势3V,内阻约为1.2Ω)
为了调节方便,测量准确,实验中应选用电流表________,滑动变阻器_________,电源___________。(填器材的符号)
(3)用测量量表示计算材料电阻率的公式是ρ = (已用刻度尺测量出接入电路中的金属导线的有效长度为l)。
查看答案和解析>>
科目:高中物理 来源:2016-2017学年山东省高二上学期期中考物理试卷(解析版) 题型:选择题
一段粗细均匀的电阻丝,横截面的直径为d ,电阻是R 。把它拉制成直径为d/10的均匀细丝后,它的电阻变成( )
A.100R B.10000R C.R/100 D.R/10000
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
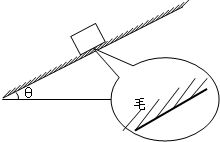 如图所示,一物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力,此时该物体与毛皮间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$.已知斜面倾斜角为θ=30°.
如图所示,一物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力,此时该物体与毛皮间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$.已知斜面倾斜角为θ=30°.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
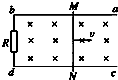 如图,两根相距为l的平行直导线ab、cd,b、d间连有一个固定电阻R,导轨电阻可忽略不计,MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN施力使它沿导轨方向以速度v做匀速运动.令U表示MN两端电压的大小,则( )
如图,两根相距为l的平行直导线ab、cd,b、d间连有一个固定电阻R,导轨电阻可忽略不计,MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN施力使它沿导轨方向以速度v做匀速运动.令U表示MN两端电压的大小,则( )| A. | U=$\frac{1}{2}vB$l | B. | U=$\frac{1}{3}$vBl | C. | U=vBl | D. | U=2vBl |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
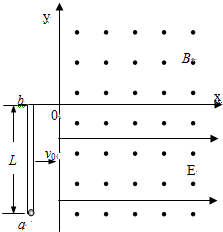 在一足够大的光滑水平面上建立如图所示的xoy坐标系,第一、四象限存在方向竖直向上、磁感应强度为B的匀强磁场;第四象限存在沿x轴正方向、电场强度为E的匀强电场.一长为L内壁光滑的薄玻璃管与y轴平行放置在水平面上的第三象限,开口端b与x轴重合,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管带着小球以水平速度v0沿x轴正方向运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从y轴飞离磁场.设运动过程中小球的电荷量保持不变,求:
在一足够大的光滑水平面上建立如图所示的xoy坐标系,第一、四象限存在方向竖直向上、磁感应强度为B的匀强磁场;第四象限存在沿x轴正方向、电场强度为E的匀强电场.一长为L内壁光滑的薄玻璃管与y轴平行放置在水平面上的第三象限,开口端b与x轴重合,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管带着小球以水平速度v0沿x轴正方向运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从y轴飞离磁场.设运动过程中小球的电荷量保持不变,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
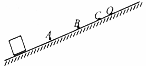 如图所示,在粗糙斜面上有一个质量为m的小物体,某时刻给它一个初速度,使其沿斜面向上做匀减速直线运动,依次经过A、B、C三点后停在O点,A、B、C三点到O点的距离分别为L1、L2、L3,为小物块由A、B、C三点运动到O点所用的时间分别为t1、t2、t3,则下列结论正确的是( )
如图所示,在粗糙斜面上有一个质量为m的小物体,某时刻给它一个初速度,使其沿斜面向上做匀减速直线运动,依次经过A、B、C三点后停在O点,A、B、C三点到O点的距离分别为L1、L2、L3,为小物块由A、B、C三点运动到O点所用的时间分别为t1、t2、t3,则下列结论正确的是( )| A. | $\frac{{L}_{1}}{{t}_{1}}$=$\frac{{L}_{2}}{{t}_{2}}$=$\frac{{L}_{3}}{{t}_{3}}$ | B. | $\frac{{L}_{1}}{{t}_{1}^{2}}$=$\frac{{L}_{2}}{{t}_{2}^{2}}$=$\frac{{L}_{3}}{{t}_{3}^{2}}$ | ||
| C. | $\frac{{L}_{1}}{{t}_{1}}$<$\frac{{L}_{2}}{{t}_{2}}$<$\frac{{L}_{3}}{{t}_{3}}$ | D. | $\frac{{L}_{1}}{{t}_{1}^{2}}$<$\frac{{L}_{2}}{{t}_{2}^{2}}$<$\frac{{L}_{3}}{{t}_{3}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com