
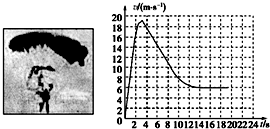
 总质量为80kg的跳伞运动员从离地500m高的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图象,根据图象可知(g取10m/s2)
总质量为80kg的跳伞运动员从离地500m高的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图象,根据图象可知(g取10m/s2)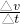 =
= m/s2=8m/s2.故A正确.
m/s2=8m/s2.故A正确.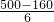 s=70.7s.故C错误.
s=70.7s.故C错误.

科目:高中物理 来源: 题型:
 (2009?惠州二模)总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)
(2009?惠州二模)总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
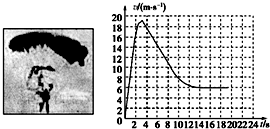 总质量为80kg的跳伞运动员从离地500m高的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图象,根据图象可知(g取10m/s2)( )
总质量为80kg的跳伞运动员从离地500m高的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图象,根据图象可知(g取10m/s2)( )查看答案和解析>>
科目:高中物理 来源: 题型:
 总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)
总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
 总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)
总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
 ?
?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com