
 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )| A. | 球的速度v等于L$\sqrt{\frac{g}{2H}}$ | |
| B. | 球从击球点至落地点的动能减少了$\frac{1}{2}$mv2 | |
| C. | 球从击球点至落地点的重力势能减少了mgH | |
| D. | 球从击球点至落地点的机械能减少了mgH+$\frac{1}{2}$mv2 |
分析 根据平抛运动的高度求出运动的时间,结合水平位移和时间求出球的初速度.球在运动过程中,只有重力做正功,动能增加,重力势能减小,机械能不变.
解答 解:A、球做平抛运动,根据H=$\frac{1}{2}$gt2得,平抛运动的时间 t=$\sqrt{\frac{2H}{g}}$,则球平抛运动的初速度 v=$\frac{L}{t}$=L$\sqrt{\frac{g}{2H}}$,故A正确.
B、球从击球点至落地点的过程中,重力做功为mgH,由动能定理知,球的动能增加mgH,故B错误.
C、球从击球点至落地点的过程中,重力做功为mgH,则重力势能减少了mgH,故C正确.
D、球从击球点至落地点的过程中,只有重力做功,机械能不变,故D错误.
故选:AC
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活解题.要掌握机械能守恒的条件:只有重力或弹力做功.


科目:高中物理 来源: 题型:多选题
| A. | Pt | B. | (f+ma)l | C. | $\frac{1}{2}$mvm2 | D. | $\frac{1}{2}$mvm2+fl |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )
如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )| A. | 只要满足l2≥$\sqrt{({l}_{1}+h)^{2}+{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| B. | 只要满足l3≥$\sqrt{({l}_{1}+h)^{2}+4{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| C. | 糖果可能以$\frac{mg{{l}_{2}}^{2}}{{d}^{2}}$($\sqrt{{{l}_{2}}^{2}-{d}^{2}}$-l1)的初动能开始绕中间悬点做圆运动 | |
| D. | 糖果到达最低点的动能可能等于mg[l2-$\frac{({{l}_{2}}^{2}-{d}^{2})^{\frac{3}{2}}}{{{l}_{2}}^{2}}$-$\frac{{l}_{1}{d}^{2}}{{{l}_{2}}^{2}}$] |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
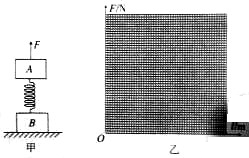 质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接,将它们竖直静止放在水平面上,如图甲所示,现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40s物体B刚要离开地面.取g=10m/s2
质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接,将它们竖直静止放在水平面上,如图甲所示,现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40s物体B刚要离开地面.取g=10m/s2查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,半径为R的光滑圆环竖直放置,在环上套有小球A和B,A、B之间用一根长为2R的轻杆相连,并使小球能在环上自由滑动.已知A球质量为3m,B球质量为m,重力加速度为g,使小球从与圆心O等高处静止释放,在A球从初始位置滑到圆环最低点的过程中,轻杆对B球做的功为( )
如图所示,半径为R的光滑圆环竖直放置,在环上套有小球A和B,A、B之间用一根长为2R的轻杆相连,并使小球能在环上自由滑动.已知A球质量为3m,B球质量为m,重力加速度为g,使小球从与圆心O等高处静止释放,在A球从初始位置滑到圆环最低点的过程中,轻杆对B球做的功为( )| A. | mgR | B. | 1.5mgR | C. | 2mgR | D. | 3mgR |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 在“研究电磁感应现象“”的实验中.
在“研究电磁感应现象“”的实验中.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 光滑斜面AB足够长,斜面倾角为θ=30°,斜面底端A处固定一挡板,现让物块1、2先后从A处以相同的初速度v=10m/s沿斜面向上运动,时间间隔T=2s,物块1、2质量分别为m1=2kg,m2=3kg.假设不考虑空气阻力,物块1、2间及物块2与挡板间的碰撞为弹性碰撞.且碰撞时间极短.g取10m/s2.求物块1、2第一次碰撞后瞬间各自的速度v1,v2.
光滑斜面AB足够长,斜面倾角为θ=30°,斜面底端A处固定一挡板,现让物块1、2先后从A处以相同的初速度v=10m/s沿斜面向上运动,时间间隔T=2s,物块1、2质量分别为m1=2kg,m2=3kg.假设不考虑空气阻力,物块1、2间及物块2与挡板间的碰撞为弹性碰撞.且碰撞时间极短.g取10m/s2.求物块1、2第一次碰撞后瞬间各自的速度v1,v2.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 物理学家在研究物理问题时,常常抓住问题的主要因素,忽略问题的次要因素,从而抽象出一个物理模型.比如,在高中阶段研究有关弹簧的问题时,由于弹簧本身质量很小,所以将弹簧抽象为质量不计的轻弹簧.为了探讨这种研究问题方法的可行性,我们以下面的问题为例进行探究.如图所示,水平光滑地面 上放有两个滑块A和B,质量分别为m和2m,其中B滑块上安装一只质量很小的轻弹簧,现给A一个初速度,大小为v0,则:
物理学家在研究物理问题时,常常抓住问题的主要因素,忽略问题的次要因素,从而抽象出一个物理模型.比如,在高中阶段研究有关弹簧的问题时,由于弹簧本身质量很小,所以将弹簧抽象为质量不计的轻弹簧.为了探讨这种研究问题方法的可行性,我们以下面的问题为例进行探究.如图所示,水平光滑地面 上放有两个滑块A和B,质量分别为m和2m,其中B滑块上安装一只质量很小的轻弹簧,现给A一个初速度,大小为v0,则:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 所有行星绕太阳运动的轨道都是椭圆 | |
| B. | 太阳处在所有行星轨道的中心上 | |
| C. | 任一行星与太阳的连线在相等时间内扫过相等的面积 | |
| D. | 所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com