
 如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )
如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )| A. | 只要满足l2≥$\sqrt{({l}_{1}+h)^{2}+{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| B. | 只要满足l3≥$\sqrt{({l}_{1}+h)^{2}+4{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| C. | 糖果可能以$\frac{mg{{l}_{2}}^{2}}{{d}^{2}}$($\sqrt{{{l}_{2}}^{2}-{d}^{2}}$-l1)的初动能开始绕中间悬点做圆运动 | |
| D. | 糖果到达最低点的动能可能等于mg[l2-$\frac{({{l}_{2}}^{2}-{d}^{2})^{\frac{3}{2}}}{{{l}_{2}}^{2}}$-$\frac{{l}_{1}{d}^{2}}{{{l}_{2}}^{2}}$] |
分析 糖果通过正下方第一颗星星前,绳2和绳3不能绷紧;绕中间点作圆周运动时,绳1被切断,绳2绷紧时有速度损失,可以由初态到绳2绷紧前使用动能定理求解;最低点之前可能有两次速度损失.
解答 解:AB、将最左侧的绳子割断,糖果在绳子拉直前做自由落体运动,绳2和绳3不能绷紧,后绕绳做圆周运动,则绕l2运动而l3未伸直,或绕l3运动而l2未伸直,要使就能经过正下方第一颗星星处,l2和l3需要同时满足的条件是:l2≥$\sqrt{({l}_{1}+h)^{2}+{d}^{2}}$和l3≥$\sqrt{({l}_{1}+h)^{2}+4{d}^{2}}$,故A、B错误;
C、若l3足够长,将最左侧的绳子割断,糖果自由下落h=($\sqrt{{l}_{2}^{2}-{d}^{2}}-{l}_{1}$)后l2刚刚伸直,糖果竖直下落h=($\sqrt{{l}_{2}^{2}-{d}^{2}}-{l}_{1}$)后速度为 v=$\sqrt{2gh}$,方向竖直向下.
此时绳2绷紧后,沿绳方向的分速度即刻减为零,剩余垂直于绳子方向的速度,为 v1=v•$\frac{d}{{l}_{2}}$
开始绕中间悬点做圆周运动的初动能 Ek1=$\frac{1}{2}m{v}_{1}^{2}$
联立解得 Ek1=$\frac{mg{d}^{2}}{{l}_{2}^{2}}$($\sqrt{{l}_{2}^{2}-{d}^{2}}-{l}_{1}$).故C错误.
D、以C选项为初态,以糖果刚刚到达最低点为末态,由动能定理得 mg(l3-$\sqrt{{l}_{2}^{2}-{d}^{2}}$)=Ek-$\frac{1}{2}m{v}_{1}^{2}$,解得:Ek=mg[l3-$\frac{({{l}_{2}}^{2}-{d}^{2})^{\frac{3}{2}}}{{{l}_{2}}^{2}}$-$\frac{{l}_{1}{d}^{2}}{{{l}_{2}}^{2}}$],由于绳子绷紧过程可能有两次速度损失而产生能量损失,故绷紧后动能会少于Ek,故D正确.
故选:D
点评 本题的关键要分析糖果的运动过程,运用几何关系研究下落的高度,运用动能定理求解速度.要注意绳子绷紧过程动能有损失.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题
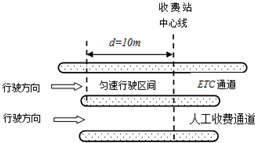 我国ETC联网正式启动运行,ETC是电子不停车收费系统的简称.汽车分别通过ETC通道和人工收费通道的流程如图所示.假设汽车以v1=15m/s朝收费站正常沿直线行驶,如果通过ETC通道,需要在收费站中心线前l0m处正好匀减速至v2=5m/s,匀速通过中心线后,再匀加速至v1正常行驶;如果通过人工收费通道,需要匀减速至中心线处停下,经过15s缴费成功后,再启动汽车匀加速至v1正常行驶.设汽车加速和减速过程中的加速度大小均为l m/s2.求:
我国ETC联网正式启动运行,ETC是电子不停车收费系统的简称.汽车分别通过ETC通道和人工收费通道的流程如图所示.假设汽车以v1=15m/s朝收费站正常沿直线行驶,如果通过ETC通道,需要在收费站中心线前l0m处正好匀减速至v2=5m/s,匀速通过中心线后,再匀加速至v1正常行驶;如果通过人工收费通道,需要匀减速至中心线处停下,经过15s缴费成功后,再启动汽车匀加速至v1正常行驶.设汽车加速和减速过程中的加速度大小均为l m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在研究摩擦力特点的实验中,将木块放在水平木板上,木板放在光滑地水平面上,如图甲所示,将木块固定,用力沿水平方向拉木板,拉力从0开始逐渐增大.分别用力传感器采集拉力和木块受到的摩擦力,并用计算机绘制出摩擦力,随拉力F变化的图象,如图乙所示.已知木块质量为0.78kg,木板质量为1.04kg.(重力加速度g取10m/s2)正确的是( )
在研究摩擦力特点的实验中,将木块放在水平木板上,木板放在光滑地水平面上,如图甲所示,将木块固定,用力沿水平方向拉木板,拉力从0开始逐渐增大.分别用力传感器采集拉力和木块受到的摩擦力,并用计算机绘制出摩擦力,随拉力F变化的图象,如图乙所示.已知木块质量为0.78kg,木板质量为1.04kg.(重力加速度g取10m/s2)正确的是( )| A. | 此实验方法与教材中不一致,是错误的 | |
| B. | 此实验方法可行,可算出动摩擦因数是0.4 | |
| C. | 此实验方法可行,可算出动摩擦因数是0.3 | |
| D. | 上述说法均不正确 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
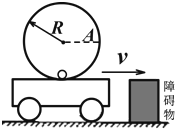 如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )| A. | 铅球能上升的最大高度一定等于$\frac{{v}^{2}}{2g}$ | |
| B. | 无论v多大,铅球上升的最大高度不超过$\frac{{v}^{2}}{2g}$ | |
| C. | 要使铅球一直不脱离圆桶,v的最小速度为$\sqrt{5gR}$ | |
| D. | 若铅球能到达圆桶最高点,则铅球在最高点的速度大小可以等于零 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知球的质量为m,底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列叙述正确的是( )| A. | 球的速度v等于L$\sqrt{\frac{g}{2H}}$ | |
| B. | 球从击球点至落地点的动能减少了$\frac{1}{2}$mv2 | |
| C. | 球从击球点至落地点的重力势能减少了mgH | |
| D. | 球从击球点至落地点的机械能减少了mgH+$\frac{1}{2}$mv2 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
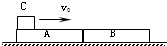 在光滑的水平面上,并排放置着两个质量为m、长L的完全相同的A、B长木板.一质量为2m的小滑块,以一定的初速度v0,从左侧冲上木板A,滑块与木板间的动摩擦因数为μ,要使滑块最终能停在木板B上,并以$\frac{5}{9}$v0的速度共同运动.重力加速度为g,求:
在光滑的水平面上,并排放置着两个质量为m、长L的完全相同的A、B长木板.一质量为2m的小滑块,以一定的初速度v0,从左侧冲上木板A,滑块与木板间的动摩擦因数为μ,要使滑块最终能停在木板B上,并以$\frac{5}{9}$v0的速度共同运动.重力加速度为g,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com