
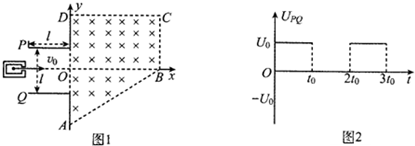
���� ��1�����������֪��������ƽ�а������ƽ���˶�����ƽ���˶����ʿɷֱ��������ˮƽ�������ֱ������ٶȣ������������ٶȽ��кϳɣ������ٶ�Ϊʸ����ע�ⷽ�����⣻
��2���軭�������˶��켣�����ݼ���֪ʶ��������˶��뾶��������Ÿ�Ӧǿ�ȵĴ�С���ɼ���֪ʶ�����AB�߳����������ų����������
��3�����ж������ڴų����˶��켣������Բ���˶���ʽ������ӵ��˶�ʱ�䣮
��� 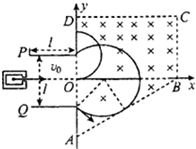 �⣺��1��t=0ʱ�̽���糡��������t0ʱ������糡���ڵ糡����ƽ�ף�
�⣺��1��t=0ʱ�̽���糡��������t0ʱ������糡���ڵ糡����ƽ�ף�
ˮƽ����${t_0}=\frac{l}{v_0}$
��ֱ����$y=\frac{1}{2}\frac{{{U_0}q}}{lm}t_0^2=\frac{l}{2}$
�ڵ糡���˶������ܶ�����$q\frac{U_0}{l}y=\frac{1}{2}m{v^2}-\frac{1}{2}mv_0^2$
����ٶȴ�С��$v=\sqrt{2}{v_0}=\frac{{\sqrt{2}l}}{t_0}$
�ٶȷ�����ˮƽ�����45��
��2���ٽ�켣��ͼ��ʾ���������ڴų���Բ���˶��İ뾶r1��
�ɼ��ι�ϵ��${r_1}=\frac{l}{{2cos{{45}^0}}}=\frac{{\sqrt{2}}}{2}l$
�����ڴų����˶���$qvB=m\frac{v^2}{r_1}$
���$B=\frac{mv}{{q{r_1}}}=\frac{2m}{{q{t_0}}}$
��AB��Ϊa���м��ι�ϵ��$\overline{OB}=\frac{r_1}{{sin{{30}^0}}}+\frac{l}{2}tan{45^0}=asin{60^0}$
���$a=\frac{{2\sqrt{6}+\sqrt{3}}}{3}l$
�ų�����������$S=\frac{1}{4}{a^2}sin{60^0}+\frac{1}{2}{a^2}sin{60^0}=\frac{{9\sqrt{3}+4\sqrt{6}}}{8}{l^2}$
��3��t0ʱ�̽��������Ĵ��������������������ֱ���˶�����2t0ʱ����x�������ų��������ų�������Բ���˶��İ뾶r2����$q{v_0}B=m\frac{v_0^2}{r_2}$
���${r_2}=\frac{{m{v_0}}}{qB}=\frac{l}{2}$
��$\frac{a}{2}��l=2{r_2}$֪�����ӽ���OD������ų�
�����ڴų����˶�������$T=\frac{{2��{r_2}}}{v_0}=��{t_0}$
�����ڴų����˶���ʱ��$t=\frac{T}{2}=\frac{{��{t_0}}}{2}$
�𣺣�1��t=0ʱ�̽��������Ĵ�����������ų�ʱ���ٶȴ�СΪ$\frac{\sqrt{2}l}{{t}_{0}}$��������ˮƽ�����45�㣻
��2����ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�С���ų���������$\frac{9\sqrt{3}+4\sqrt{6}}{8}{l}^{2}$��
��3��t=t0ʱ�̽��������Ĵ�����������ǿ�ų����˶���ʱ��Ϊ$\frac{��{t}_{0}}{2}$��
���� �������ڴ�����������ϳ��е��˶�����Ҫ���鿼���ۺϷ����������������Ĺؼ����ҵ����ӵ��˶��켣�պú�AB�����У��ҵ����ι�ϵ���AB�ߵij��ȣ�����Ϊѹ���⣬��ѧ������Ҫ��ܸߣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
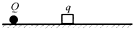 ��ͼ��ʾ���ڴֲڡ���Ե���㹻���ˮƽ���Ϲ̶���һ��������ɵĵ���Q����һ������Ϊm�����Ϊq��С�����飨��������Կ���Ϊ�ʵ㣩����ˮƽ���ϲ��ɾ�ֹ�ͷţ������齫��ˮƽ������Զ��Q�ķ���ʼ�˶������ڽ������˶������������У�������
��ͼ��ʾ���ڴֲڡ���Ե���㹻���ˮƽ���Ϲ̶���һ��������ɵĵ���Q����һ������Ϊm�����Ϊq��С�����飨��������Կ���Ϊ�ʵ㣩����ˮƽ���ϲ��ɾ�ֹ�ͷţ������齫��ˮƽ������Զ��Q�ķ���ʼ�˶������ڽ������˶������������У�������| A�� | �糡���Խ��������Ĺ����ڽ��������ӵĻ�е�� | |
| B�� | ������ĵ�����һֱ���� | |
| C�� | ������ļ��ٶ���������С | |
| D�� | �糡�Խ����������Ĺ�һ������Ħ���������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
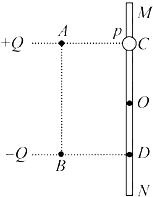 ��ͼ��ʾ���̶���ͬһ����ֱ���ϵ�A��B���������������ֵ�ɵĵ��ɣ�������ֱ�Ϊ+Q��-Q��A��B���Ϊ2d��MN����ֱ���õĹ⻬��Եϸ�ˣ�����һ������ϸ�˵Ĵ���С��p������Ϊm�������Ϊ+q������Ϊ���ɣ���Ӱ��糡�ķֲ������ֽ�С��p�������A�ȸߵ�C���ɾ�ֹ��ʼ�ͷţ�С��p�����˶�����C�����Ϊd��O��ʱ���ٶ�Ϊv����֪MN��AB֮��ľ���Ϊd������������Ϊk���������ٶ�Ϊg���������֪��Ϣ�ܶ����õ����������ǣ�������
��ͼ��ʾ���̶���ͬһ����ֱ���ϵ�A��B���������������ֵ�ɵĵ��ɣ�������ֱ�Ϊ+Q��-Q��A��B���Ϊ2d��MN����ֱ���õĹ⻬��Եϸ�ˣ�����һ������ϸ�˵Ĵ���С��p������Ϊm�������Ϊ+q������Ϊ���ɣ���Ӱ��糡�ķֲ������ֽ�С��p�������A�ȸߵ�C���ɾ�ֹ��ʼ�ͷţ�С��p�����˶�����C�����Ϊd��O��ʱ���ٶ�Ϊv����֪MN��AB֮��ľ���Ϊd������������Ϊk���������ٶ�Ϊg���������֪��Ϣ�ܶ����õ����������ǣ�������| A�� | O�㴦�ĵ糡ǿ��E | |
| B�� | C��O��ĵ��Ʋ�UCO | |
| C�� | С��p���������B�ȸߵ�D��ʱ���ٶ�V | |
| D�� | С��p�������˶���C��D��ʱ��T |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
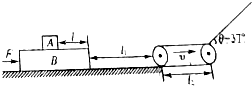 ��ͼ��ʾ���ڹ⻬��ˮƽ������һ����Ϊ2m���㹻���ij�ľ��B�����ϱ����볤ľ��B���Ҷ˾���Ϊl=0.7m����һ����Ϊm�����A������Ϊ�ʵ㣩����ľ���봫�ʹ����ľ���Ϊl1=3.2m���Ҵ��ʹ����϶��볤ľ��B���ϱ�����ƽ�룮�ָ���ľ��Bһ��ˮƽ���ң���СΪF=$\frac{3}{2}$��mg������������ľ��B�봫�ʹ����������˲�䣬��ľ��B����ֹͣ�ҹ̶�������ͬʱ��ȥ��F�����A��ijһ�ٶȻ�����˳ʱ������ת�����ٶ�Ϊv��δ֪��������Ϊl2=0.5m�Ĵ��ʹ�������ˮƽ��н�Ϊ��=37����㹻����б�棬�����A��б�����ϻ����̵�λ����ʱ���ϵΪs=kt-5t2��m����k��0����֪���A�볤ľ��B�����ʹ���б��֮��Ķ�Ħ��������Ϊ�̣����ʹ�ת���ִ�С���Բ��ƣ�����Aͨ������νӴ�ʱ��������ʧ���������ٶ�ȡg=10m/s2������֪sin37��=0.6��cos37��=0.8��
��ͼ��ʾ���ڹ⻬��ˮƽ������һ����Ϊ2m���㹻���ij�ľ��B�����ϱ����볤ľ��B���Ҷ˾���Ϊl=0.7m����һ����Ϊm�����A������Ϊ�ʵ㣩����ľ���봫�ʹ����ľ���Ϊl1=3.2m���Ҵ��ʹ����϶��볤ľ��B���ϱ�����ƽ�룮�ָ���ľ��Bһ��ˮƽ���ң���СΪF=$\frac{3}{2}$��mg������������ľ��B�봫�ʹ����������˲�䣬��ľ��B����ֹͣ�ҹ̶�������ͬʱ��ȥ��F�����A��ijһ�ٶȻ�����˳ʱ������ת�����ٶ�Ϊv��δ֪��������Ϊl2=0.5m�Ĵ��ʹ�������ˮƽ��н�Ϊ��=37����㹻����б�棬�����A��б�����ϻ����̵�λ����ʱ���ϵΪs=kt-5t2��m����k��0����֪���A�볤ľ��B�����ʹ���б��֮��Ķ�Ħ��������Ϊ�̣����ʹ�ת���ִ�С���Բ��ƣ�����Aͨ������νӴ�ʱ��������ʧ���������ٶ�ȡg=10m/s2������֪sin37��=0.6��cos37��=0.8���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
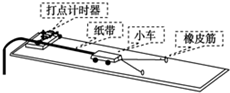 ����ͼ��ʾ������̽���������ٶȱ仯�Ĺ�ϵ��
����ͼ��ʾ������̽���������ٶȱ仯�Ĺ�ϵ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
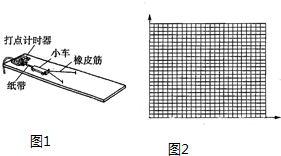 һ����ʵ��С��Ϊ�ˡ�̽�������ٶȱ仯�Ĺ�ϵ�����������ͼ1��ʾ��ʵ�飬������ʱ���̶��ڳ�ľ�����ˣ�ֽ��������С���ϲ���������ʱ������ʹС���������ʱ����һ�ξ��룬ͨ�������ں��ʵ�λ����ͼ������Ƥ��̶��ڳ�ľ���ϣ���һ�˹���С���ϣ�ʹ��Ƥ�����Ȼ���ȣ�Ȼ��ľ�������ʵ������ƽ��Ħ�����������������С����ʹС���ɾ�ֹ�ͷţ�������Ƥ���������ʹС���س�ľ���˶���ͨ������ʱ�������ֽ������С������ʱ���ٶȣ��������������Ƥ�������������֤ÿ���ͷ�С����λ����ͬ����ÿ�β������������ݼ�¼��
һ����ʵ��С��Ϊ�ˡ�̽�������ٶȱ仯�Ĺ�ϵ�����������ͼ1��ʾ��ʵ�飬������ʱ���̶��ڳ�ľ�����ˣ�ֽ��������С���ϲ���������ʱ������ʹС���������ʱ����һ�ξ��룬ͨ�������ں��ʵ�λ����ͼ������Ƥ��̶��ڳ�ľ���ϣ���һ�˹���С���ϣ�ʹ��Ƥ�����Ȼ���ȣ�Ȼ��ľ�������ʵ������ƽ��Ħ�����������������С����ʹС���ɾ�ֹ�ͷţ�������Ƥ���������ʹС���س�ľ���˶���ͨ������ʱ�������ֽ������С������ʱ���ٶȣ��������������Ƥ�������������֤ÿ���ͷ�С����λ����ͬ����ÿ�β������������ݼ�¼��| ���� ��Ƥ���������Ƥ������� | ��Ƥ�����Ĺ� | 10�����ľ���x��m�� | 10������ʱ��T��s�� | С����õ��ٶ�vn | С���ٶȵ�ƽ��vn2 |
| 1 | W | 0.200 | 0.2 | 1.00 | 1.00 |
| 2 | 0.280 | 0.2 | 1.40 | 1.96 | |
| 3 | 0.300 | 0.2 | 1.50 | 2.25 | |
| 4 | 0.400 | 0.2 | 2.00 | 4.00 | |
| 5 | 0.450 | 0.2 | 2��25 | 5.06 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

| ���� | M/kg | ��v22-v12��/m2s-2 | ��Ek/J | F/N | W/J |
| 1 | 0.500 | 0.760 | 0.190 | 0.400 | 0.200 |
| 2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
| 3 | 0.500 | 2.40 | ��E3 | 1.22 | W3 |
| 4 | 1.00 | 2.40 | 1.20 | 2.42 | 1.21 |
| 5 | 1.00 | 2.84 | 1.42 | 2.86 | 1.43 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com