
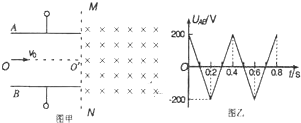
分析 (1)在t=0.ls时刻射入电场的带电粒子,在电场中做匀速直线运动,进入磁场做圆周运动,垂直边界进入磁场,知运动半个圆周射出,在MN上射入点和射出点的距离为2R.
(2)带电粒子从极板的边缘射出电场时速度最大,根据带电粒子在磁场中做类平抛运动,根据沿电场方向上的匀加速直线运动,求出偏转的电压,根据动能定律求出射出电场的最大速度.
(3)在t=0.25s时偏转电压为100V,根据第二问解出的结论知,粒子贴着上边缘进入磁场,根据v=$\sqrt{2}{v}_{0}$,知垂直进入磁场时与磁场边界的夹角为$\frac{π}{4}$,射出磁场时与磁场边界的夹角也为$\frac{π}{4}$,故对应的圆心角为$\frac{1}{2}π$,根据t=$\frac{θ}{2π}T$求出运动的时间.
解答 解:(1)在t=0.1s时刻射入电场的带电粒子,在极板间做匀速直线运动,以v0垂直磁场边界垂直射入磁场,由qvB=$\frac{m{v}^{2}}{R}$可得:
$R=\frac{mv}{qB}=0.2$m
在MN上的入射点和出磁场时在MN上的出射点间的距离为:d=2R=0.4m
(2)设带电粒子从极板的边缘射出电场时的速度最大,对应的瞬时电压为u0,则:$\frac{1}{2}d=\frac{1}{2}\frac{q{u}_{0}}{md}(\frac{L}{{v}_{0}})^{2}$
解得:u0=100V
由动能定理:$\frac{1}{2}m{v}^{2}=\frac{1}{2}m{v}_{0}^{2}+\frac{1}{2}q{u}_{0}$
射出的最大速度:$v=\sqrt{2}{v}_{0}=\sqrt{2}×1{0}^{5}$m/s
(3)在T=0.25S时刻从电场射出的带电粒子,从极板的上边缘射出电场,垂直进入磁场时与磁场边界的夹角为$\frac{π}{4}$,射出磁场时与磁场边界的夹角也为$\frac{π}{4}$,故对应的圆周的圆心角为$\frac{1}{2}π$,故在磁场中运动的时间为圆周运动周期的四分之一.
由qvB=$\frac{m{v}^{2}}{R}$,$T=\frac{2πr}{v}$
得到:$T=\frac{2πm}{qB}$,
得:$t=\frac{1}{4}T=1.57×1{0}^{-5}$s
答:(1)在t=0.1s时刻射入电场的带电粒子,进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为0.4m;
(2)带电粒子射出电场时的最大速度是$\sqrt{2}×1{0}^{5}$m/s;
(3)在t=0.25s时刻从电场射出的带电粒子,在磁场中运动的时间是1.57×10-5s.
点评 解决本题的关键理清粒子在电场中和磁场中的运动轨迹,结合运动学公式、牛顿第二定律和动能定理进行求解.


科目:高中物理 来源: 题型:选择题
 如图所示,美洲狮是一种凶猛的食肉猛兽,也是噬杀成性的“杂食家”在跳跃方面有着惊人的“天赋”,它“厉害的一跃”水平距离可达44英尺,高达11英尺,设美洲狮做“厉害的一跃”离开地面时的速度方向与水平面的夹角为α,若不计空气阻力,美洲狮可看做质点,则tanα等于( )
如图所示,美洲狮是一种凶猛的食肉猛兽,也是噬杀成性的“杂食家”在跳跃方面有着惊人的“天赋”,它“厉害的一跃”水平距离可达44英尺,高达11英尺,设美洲狮做“厉害的一跃”离开地面时的速度方向与水平面的夹角为α,若不计空气阻力,美洲狮可看做质点,则tanα等于( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 3和2 | B. | 2和3 | C. | 3和3 | D. | 2和2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一个单匝矩形线圈在有界的匀强磁场中匀速转动,转动轴OO′与磁场方向垂直,线圈abcd关于转动轴对称,线圈的ab边与磁场的边界MN重合,位于图示位置时线圈平面与磁场平行.线圈的面积为S.匀强磁场的磁感应强度为B,线圈转动的角速度为ω.则下列说法中正确的是( )
如图所示,一个单匝矩形线圈在有界的匀强磁场中匀速转动,转动轴OO′与磁场方向垂直,线圈abcd关于转动轴对称,线圈的ab边与磁场的边界MN重合,位于图示位置时线圈平面与磁场平行.线圈的面积为S.匀强磁场的磁感应强度为B,线圈转动的角速度为ω.则下列说法中正确的是( )| A. | 若从图示位置开始计时,那么,线圈产生的感应电动势的瞬时值表达式为e=BSωsinωt | |
| B. | 过图示位置时,穿过线圈的磁通量为0.磁通量的变化率为BSω | |
| C. | 经过图示位置时,穿过线圈的磁通量为0.电流的方向发生改变 | |
| D. | 若线圈绕ab轴转动,那么,感应电动势的有效值为$\frac{BSω}{{\sqrt{2}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
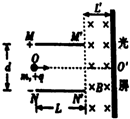 如图所示,一对平行金属板MM′、NN′水平放置.板长L=0.4m.板间距离d=0.4m.将两板接在-个电压可以调节的电源上(圈中未画出).MM′接电源的正极.在两板的右侧存在水平方向的匀强磁场.磁场的方向垂直于纸面向里.磁感应强度的大小B=0 25T.NN′在磁场的左侧边界上,磁场的右侧边界竖直放置-个足够长的光屏,磁场的宽度L′=0.2m,现有比荷为为$\frac{q}{m}$=2×105c/kg的带正电的粒子束.沿两扳的中轴线00′以相同的速度不停地射入,当两板之间的电压为0V时,粒子刚好不能打在光屏上.不计粒子重力.
如图所示,一对平行金属板MM′、NN′水平放置.板长L=0.4m.板间距离d=0.4m.将两板接在-个电压可以调节的电源上(圈中未画出).MM′接电源的正极.在两板的右侧存在水平方向的匀强磁场.磁场的方向垂直于纸面向里.磁感应强度的大小B=0 25T.NN′在磁场的左侧边界上,磁场的右侧边界竖直放置-个足够长的光屏,磁场的宽度L′=0.2m,现有比荷为为$\frac{q}{m}$=2×105c/kg的带正电的粒子束.沿两扳的中轴线00′以相同的速度不停地射入,当两板之间的电压为0V时,粒子刚好不能打在光屏上.不计粒子重力.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
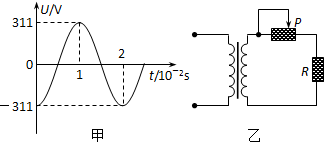
| A. | 副线圈输出电压的频率为100Hz | |
| B. | 副线圈输出电压的有效值为5V | |
| C. | P向左移动时,变压器原、副线圈的电流都减小 | |
| D. | P向左移动时,变压器的输入功率增加 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
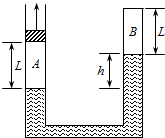 如图所示,内径粗细均匀的U形管,右侧B管上端封闭,左侧A管上端开口,管内注入水银,并在A管内装配有光滑的、质量可以不计的活塞,使两管中均封入L=25cm的空气柱,活塞上方的大气压强为P0=76cmHg,这时两管内水银面高度差h=6cm.今用外力竖直向上缓慢地拉活塞,直至使两管中水银面相平.设温度保持不变,则:A管中活塞向上移动距离是多少?
如图所示,内径粗细均匀的U形管,右侧B管上端封闭,左侧A管上端开口,管内注入水银,并在A管内装配有光滑的、质量可以不计的活塞,使两管中均封入L=25cm的空气柱,活塞上方的大气压强为P0=76cmHg,这时两管内水银面高度差h=6cm.今用外力竖直向上缓慢地拉活塞,直至使两管中水银面相平.设温度保持不变,则:A管中活塞向上移动距离是多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 ①现有按酒精与油酸的体积比为m:n 配制好的油酸酒精溶液,用滴管从量筒中取体积为V的该种溶液,让其自由滴出,全部滴完共N滴.把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面上展开,稳定后形成单分子油膜的形状如右图所示,已知坐标纸上每个小方格面积为S.根据以上数据可估算出油酸分子直径为d=$\frac{nV}{8Ns(m+n)}$;
①现有按酒精与油酸的体积比为m:n 配制好的油酸酒精溶液,用滴管从量筒中取体积为V的该种溶液,让其自由滴出,全部滴完共N滴.把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面上展开,稳定后形成单分子油膜的形状如右图所示,已知坐标纸上每个小方格面积为S.根据以上数据可估算出油酸分子直径为d=$\frac{nV}{8Ns(m+n)}$;查看答案和解析>>
科目:高中物理 来源: 题型:多选题
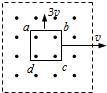 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以3v、v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以3v、v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )| A. | 导体框中产生的感应电流方向相同 | B. | 导体框中产生的焦耳热相同 | ||
| C. | 导体框ad边两端电势差相同 | D. | 通过导体框截面的电量相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com