
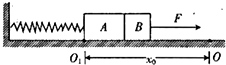
 ��ͼ��ʾ������ϵ��Ϊk��ˮƽ�ᵯ����˹̶����Ҷ�ϵס����Ϊm�����A������Ҳ��m�����B��A����һ��ճ������ʱ���ɴ�����Ȼ״̬�����ɵ��Ҷ˴���O�����Ϸ��������������������Bʹ���ɻ���ѹ������x0�ɵ��Ҷ˴���O1�����Ϸ������ͻȻ��������Ϊˮƽ���ҵĺ㶨����F������B�ϣ�A��B��ˮƽ���������˶�����A��B������Ķ�Ħ�������ֱ�Ϊ2�̡��̣�F=1.5��mg��x0=$\frac{4��mg}{k}$��A��B����Ϊ�ʵ㣬������˵����ȷ���ǣ�������
��ͼ��ʾ������ϵ��Ϊk��ˮƽ�ᵯ����˹̶����Ҷ�ϵס����Ϊm�����A������Ҳ��m�����B��A����һ��ճ������ʱ���ɴ�����Ȼ״̬�����ɵ��Ҷ˴���O�����Ϸ��������������������Bʹ���ɻ���ѹ������x0�ɵ��Ҷ˴���O1�����Ϸ������ͻȻ��������Ϊˮƽ���ҵĺ㶨����F������B�ϣ�A��B��ˮƽ���������˶�����A��B������Ķ�Ħ�������ֱ�Ϊ2�̡��̣�F=1.5��mg��x0=$\frac{4��mg}{k}$��A��B����Ϊ�ʵ㣬������˵����ȷ���ǣ�������| A�� | Aͨ��O��ʱ��ʼ��B���� | |
| B�� | A����O1��O��֮���ijһλ��ʱ��ʼ��B���� | |
| C�� | A��B�����A�����������˶� | |
| D�� | A��O1����O���˶��Ĺ������ٶ���������С |
���� ��AB���弰A��B�ֱ���������������ţ�ٵڶ����ɿ���ȷ��ʱ���룬�ٸ����˶�ѧ���̽��з�������ȷ��������˶������
��� �⣺A��AB������������Ħ���������ɵ��������ã���ʼʱһ���������˶���AB���е�������AB�䵯��Ϊ��ʱ��AB�����룻��ʱ��B��ţ�ٵڶ����ɿ�֪��F-��mg=ma
��ã�a=0.5��g��
��A������֪����ţ�ٵڶ����ɿ�֪��F1-2��mg=ma����õ��ɵĵ���F1=2.5��mg���ɺ��˶��ɿ�֪x=$\frac{2.5��mg}{k}$��x0�����A��O1��O��֮���ijһλ��ʱ��ʼ��B���룻��A����B��ȷ��
C�������ɵĵ�������A�ܵ�������ʱ��A����ƽ�⣻���У�kx=2��mg��x=$\frac{2��mg}{k}$��AB����ʱ��A�ܺ�����Ȼ���ң��ʼ����������˶�����C����
D�������Ϸ�����֪��A���������˶���Ȼ���������˶������ٶ���������С����D��ȷ��
��ѡ��BD��
���� ���⿼��ţ�ٵڶ����ɵ�Ӧ�ã�Ҫ�������ѡ���о��������������������ٽ�Ϲ��̷����Ӷ���ȷ�ٶȼ����ٶȵȵı仯�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ������A��L=5m��������M=5kg������ˮƽ�����ϣ����Ҷ����������룮��A�Ͼ��Ҷ�s=3m����һ����B���ɿ����ʵ㣩��������m=2kg����֪A��B�䶯Ħ��������1=0.1��A��������B�������Ķ�Ħ��������Ϊ��2=0.2��ԭ��ϵͳ��ֹ�������ڰ���Ҷ�ʩ��һ��Сһ����ˮƽ��F����������A��ֱ����A��B�³���ų�ȥ����ʹB���ͣ�������ұ�Ե����
��ͼ��ʾ������A��L=5m��������M=5kg������ˮƽ�����ϣ����Ҷ����������룮��A�Ͼ��Ҷ�s=3m����һ����B���ɿ����ʵ㣩��������m=2kg����֪A��B�䶯Ħ��������1=0.1��A��������B�������Ķ�Ħ��������Ϊ��2=0.2��ԭ��ϵͳ��ֹ�������ڰ���Ҷ�ʩ��һ��Сһ����ˮƽ��F����������A��ֱ����A��B�³���ų�ȥ����ʹB���ͣ�������ұ�Ե�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | һ������£�Ek=$\frac{1}{2}$mv2��v������ڵ�����ٶ� | |
| B�� | ��������ͬ�������������˶������ܴ�С��ȣ������෴ | |
| C�� | ����������ͬ�������������˶�ʱ���䶯�ܲ��ϱ仯 | |
| D�� | ���ܵĴ�С��������������ٶȴ�С��������������˶������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
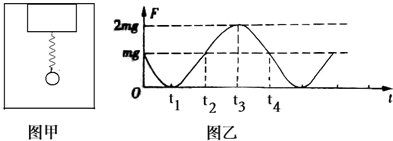
| A�� | 0-t1ʱ��С����ٶȼ�С | |
| B�� | t1-t2ʱ��С���ɺ͵�����ɵ�ϵͳ��е�ܼ��� | |
| C�� | t1-t3ʱ��С������������С | |
| D�� | t3-t4ʱ�䵯�ɵ������ܱ仯����С����С���ܱ仯����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
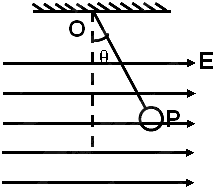 ��ͼ��ʾ��һ����Ϊm�Ĵ���С��P��һ��Եϸ��������O�㣬С��ֹ����ǿ�糡�У���֪ϸ������ֱ����ļн�Ϊ�ȣ��ȣ�45�㣩����ǿΪE������ˮƽ���ң���
��ͼ��ʾ��һ����Ϊm�Ĵ���С��P��һ��Եϸ��������O�㣬С��ֹ����ǿ�糡�У���֪ϸ������ֱ����ļн�Ϊ�ȣ��ȣ�45�㣩����ǿΪE������ˮƽ���ң����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
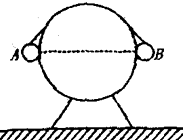
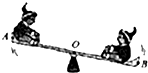 ��ͼ��ʾ�����̰��֧��Oλ�ڰ���ijһλ�ã�A��B�ǰ�������˵㣬OA��OB�������̰�ת����ijһʱ�䣬A��B�����ٶȴ�С�ֱ�ΪVA��VB�����ٶȴ�С�ֱ�Ϊ��A����B��������
��ͼ��ʾ�����̰��֧��Oλ�ڰ���ijһλ�ã�A��B�ǰ�������˵㣬OA��OB�������̰�ת����ijһʱ�䣬A��B�����ٶȴ�С�ֱ�ΪVA��VB�����ٶȴ�С�ֱ�Ϊ��A����B��������| A�� | vA��vB����A=��B | B�� | vA��vB����A=��B | C�� | vA=vB����A����B | D�� | vA=vB����A����B |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
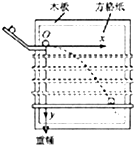 ijͬѧ��ͼʾװ�����ƽ������Ĺ켣��ʵ���Ҫ�������£�
ijͬѧ��ͼʾװ�����ƽ������Ĺ켣��ʵ���Ҫ�������£��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
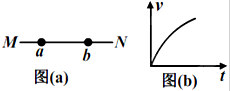 ��ͼ��a����ֱ��MN��ʾij�糡��һ���糡�ߣ�a��b�����ϵ����㣬��һ������ɵ����Ӵ�a�㴦�ɾ�ֹ�ͷţ����Ӵ�a�˶���b�����е�v-tͼ����ͼ��b����ʾ����a��b����ĵ��Ʒֱ�Ϊ��a����b����ǿ��С�ֱ�ΪEa��Eb��������a��b����ĵ����ֱܷ�ΪEPa��EPb���������������У�������
��ͼ��a����ֱ��MN��ʾij�糡��һ���糡�ߣ�a��b�����ϵ����㣬��һ������ɵ����Ӵ�a�㴦�ɾ�ֹ�ͷţ����Ӵ�a�˶���b�����е�v-tͼ����ͼ��b����ʾ����a��b����ĵ��Ʒֱ�Ϊ��a����b����ǿ��С�ֱ�ΪEa��Eb��������a��b����ĵ����ֱܷ�ΪEPa��EPb���������������У�������| A�� | ��a����b | B�� | Ea=Eb | C�� | Ea��Eb | D�� | EPa��EPb |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��A��B��С����ϸ�߿���뾶ΪR�Ĺ⻬Բ����Բ���̶��ڵ����ϣ���֪mB��mA����$\frac{m_B}{m_A}$=k��һ��ʼ������Բ�����ĵȸߣ���B���ͷź�ֱ��A����Բ������������ߵ�Ĺ����У�A������ߵ�ʱ��Bδ��أ���������
��ͼ��ʾ��A��B��С����ϸ�߿���뾶ΪR�Ĺ⻬Բ����Բ���̶��ڵ����ϣ���֪mB��mA����$\frac{m_B}{m_A}$=k��һ��ʼ������Բ�����ĵȸߣ���B���ͷź�ֱ��A����Բ������������ߵ�Ĺ����У�A������ߵ�ʱ��Bδ��أ���������| A�� | ϵͳ�������ܵļ����ǣ�mA-mB��gR | |
| B�� | ϵͳ�������ܵļ����ǣ�$\frac{��}{2}$mB-mA��gR | |
| C�� | ϵͳ���ܵ������ǣ�mA+mB��gR | |
| D�� | A��Բ������ߵ�ʱ���ٶȴ�СΪ$\sqrt{\frac{{gR��{k��-2}��}}{k+1}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com