
分析 (1)根据平抛运动知识求得月球表面的重力加速度;
(2)根据万有引力提供圆周运动向心力和月球表面重力与万有引力相等求得卫星的周期.
解答 解:(1)根据平抛的射程公式有:L=$\sqrt{\frac{2h}{g}}{v}_{0}$
可得月球表面的重力加速度为:g=$\frac{2h{v}_{0}^{2}}{{L}^{2}}$
(2)在月球表面重力与万有引力相等,月球表面附近的卫星万有引力提供圆周运动向心力有:
$G\frac{mM}{{R}^{2}}=mg=mR\frac{4{π}^{2}}{{T}^{2}}$
可得卫星的周期为:T=$2π\sqrt{\frac{R}{g}}$=$2π\sqrt{\frac{R{L}^{2}}{2h{v}_{0}^{2}}}$=$2π\frac{L}{{v}_{0}}\sqrt{\frac{R}{2h}}$
答:(1)月球表面的重力加速度为$\frac{2h{v}_{0}^{2}}{{L}^{2}}$;
(2)月球表面附近运行卫星的周期是$2π\frac{L}{{v}_{0}}\sqrt{\frac{R}{2h}}$.
点评 能根据平抛运动规律由射程和初速度求加速度,能根据万有引力提供圆周运动向心力求解卫星周期问题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中物理 来源: 题型:填空题
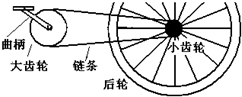 小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板(即大齿轮)转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:在时间t内脚踏板转动的圈数为N;
小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板(即大齿轮)转动的角速度,推算自行车的骑行速度.经过骑行,他得到如下的数据:在时间t内脚踏板转动的圈数为N;查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图,滑板运动员以速度v0从离地高度为h的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
如图,滑板运动员以速度v0从离地高度为h的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )| A. | v0越大,运动员在空中运动时间越长 | |
| B. | v0越大,运动员落地瞬间速度越大 | |
| C. | 运动员落地瞬间速度与高度h有关 | |
| D. | 运动员落地位置与v0大小无关 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{t}{2}$ | B. | $\frac{t}{4}$ | C. | $\frac{3t}{2}$ | D. | $\frac{{\sqrt{2}t}}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
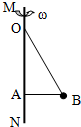 如图所示,在竖直转轴MN上距离为0.4m的O和A处分别用长0.5m和0.3m的细线连着一个质量为0.5kg的小球,使转轴通过细线带着小球转动起来.试求:
如图所示,在竖直转轴MN上距离为0.4m的O和A处分别用长0.5m和0.3m的细线连着一个质量为0.5kg的小球,使转轴通过细线带着小球转动起来.试求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 在0到t0时间内,物体速度逐渐变小 | |
| B. | 在t0时刻,物体速度增加到最大值 | |
| C. | 在0到t0时间内,物体做直线运动 | |
| D. | 在0到t0时间内,物体的速度保持不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
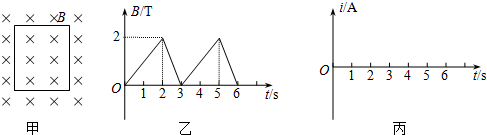
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
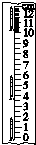 长征系列火箭为我国的卫星发射立下了汗马功劳,如图是某监测系统每隔2.5s拍摄的关于起始匀加速阶段火箭的一组照片.已知火箭的长度为40m,用刻度尺测量照片上的长度,结果如图所示.火箭的加速度a=8m/s2,火箭在照片中第2个像所对应时刻的瞬时速度大小v=42 m/s.
长征系列火箭为我国的卫星发射立下了汗马功劳,如图是某监测系统每隔2.5s拍摄的关于起始匀加速阶段火箭的一组照片.已知火箭的长度为40m,用刻度尺测量照片上的长度,结果如图所示.火箭的加速度a=8m/s2,火箭在照片中第2个像所对应时刻的瞬时速度大小v=42 m/s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com