汽车从静止开始以a=1m/s2的加速度前进,某人在车后s0=25m处同时开始以6m/s的速度匀速追汽车.
(1)经过多长时间汽车的速度达到6m/s;
(2)试通过计算判断人能否追上车;
(3)若人能追上车,则求经过多长时间人才追上车;若人不能追上车,求人、车间的最小距离.
解:(1)设车历时t其速度达到v
1=6 m/s,
则有 t=
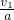
t=6 s.
(2)在t=6s之前,人的速度大于车的速度,人逐渐靠近车,t=6s之后,人的速度小于车的速度,人逐渐远离车,
在t=6s时,人车之间的距离为最近,若此时人未追上车就再也追不上车了.
t时间内
s
人=v
1t
s
人=36 m
s
车=

at
2
s
车=18 m
s
车+s
0=18+25 m=43 m
s
人小于(s
车+s
0),可见人追不上.
(3)t=6 s时,人车距离最近,△s=s
车+s
0-s
人
△s=(18+25-36)m=7 m.
答:(1)经过6s汽车的速度达到6m/s;
(2)不能追上;
(3)人、车间的最小距离为7m.
分析:(1)根据匀加速运动速度时间公式即可求解;
(2)在t=6s之前,人的速度大于车的速度,人逐渐靠近车,t=6s之后,人的速度小于车的速度,人逐渐远离车,在t=6s时,人车之间的距离为最近,若此时人未追上车就再也追不上车了.根据位移之间的关系即可判断;
(3)若追不上则t=6s时,人车距离最近,△s=s
车+s
0-s
人,若追上,根据运动学公式求出时间.
点评:这是一道追击问题,要抓住时间及位移之间的关系,理解速度相等时是追上与追不上的临界条件.

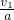
 at2
at2

 名题金卷系列答案
名题金卷系列答案