
 如图所示,海豹突击队从悬停在空中离地106米高的直升机上沿绳下滑进行速降训练.某突击队员和他携带的武器装备的总质量共为100kg,该队员轻握绳索时可获得200N的摩擦阻力,g取10m/s2.
如图所示,海豹突击队从悬停在空中离地106米高的直升机上沿绳下滑进行速降训练.某突击队员和他携带的武器装备的总质量共为100kg,该队员轻握绳索时可获得200N的摩擦阻力,g取10m/s2. =
=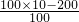 m/s2=8m/s2.
m/s2=8m/s2.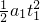 =
=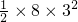 m=36m,则队员匀减速运动的位移为x2=x-x1=106m-36m=70m
m=36m,则队员匀减速运动的位移为x2=x-x1=106m-36m=70m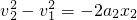
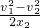 =4m/s2.
=4m/s2.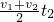 ,解得,t2=5s.
,解得,t2=5s.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中物理 来源: 题型:
 如图所示,海豹突击队从悬停在空中离地106米高的直升机上沿绳下滑进行速降训练.某突击队员和他携带的武器装备的总质量共为100kg,该队员轻握绳索时可获得200N的摩擦阻力,g取10m/s2.
如图所示,海豹突击队从悬停在空中离地106米高的直升机上沿绳下滑进行速降训练.某突击队员和他携带的武器装备的总质量共为100kg,该队员轻握绳索时可获得200N的摩擦阻力,g取10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,海豹突击队从悬停在空中离地106m高度的直升机上沿绳下滑进行速降训练.某突击队员轻握绳索时可以加速下降,为了保证着地时的安全速度不大于4m/s,在离地面70m时,该队员紧握绳索开始匀减速下降,减速下降时的加速度大小为4m/s2,突击队员以上述方式从直升机速降到地面共需要多少时间?
如图所示,海豹突击队从悬停在空中离地106m高度的直升机上沿绳下滑进行速降训练.某突击队员轻握绳索时可以加速下降,为了保证着地时的安全速度不大于4m/s,在离地面70m时,该队员紧握绳索开始匀减速下降,减速下降时的加速度大小为4m/s2,突击队员以上述方式从直升机速降到地面共需要多少时间?查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:2012-2013学年上海市浦东新区高一(上)期末物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com