
 2016��10��7�ա��й��¸���������ܾ����ڱ�������Ļ���������ҽ������塰��֮�ӡ����غ��ɹ���ڣ����ֽ�Ŀ����Ƶġ���ʦս��������������бֱ������˶�����ʦ����ս�����°�ť��ս�����ɾ�ֹ��ʼ�س�10��б��嵽ѧԱ��ǰ�����ոպ�ͣ��б���ĩ�ˣ��˹�����ʱԼ4�룮��ս���˶������У�����˵����ȷ���ǣ�������
2016��10��7�ա��й��¸���������ܾ����ڱ�������Ļ���������ҽ������塰��֮�ӡ����غ��ɹ���ڣ����ֽ�Ŀ����Ƶġ���ʦս��������������бֱ������˶�����ʦ����ս�����°�ť��ս�����ɾ�ֹ��ʼ�س�10��б��嵽ѧԱ��ǰ�����ոպ�ͣ��б���ĩ�ˣ��˹�����ʱԼ4�룮��ս���˶������У�����˵����ȷ���ǣ�������| A�� | ��ʦ����ʧ��״̬ | |
| B�� | ս������б���������ȱ���ֱ���˶� | |
| C�� | ����������Ϣ���Թ��㵼ʦ�˶���ƽ���ٶ� | |
| D�� | ս����������ʼ�ղ��� |
���� ��ȷ���⣬�����֪������ʦս�����ȼ��ٺ���٣���ϳ��˶����ص�������ij�����ʧ�ء����������Լ�ƽ���ٶȣ�
��� �⣺A�������֪������ʦս������б��ķ����ȼ��ٺ���٣����ٵĹ���������б�����µķּ��ٶȣ�������ʧ��״̬����������ʱ���������ϵķּ��ٶȣ������ڳ���״̬����A����
B����ʦս������б��ķ����ȼ��ٺ���٣��ʲ����ȱ���ֱ���˶�����B����
C����֪����λ�ƺ�ʱ�䣬�ʿ�������ƽ���ٶȹ�ʽ���ƽ���ٶȣ���C��ȷ��
D�������֪������ʦս������б��ķ����ȼ��ٺ���٣����ţ�ٵڶ����ɿ�֪�����ܵ��ĺ���������б�����£�����б�����ϣ�������һ���ᷢ���仯����D����
��ѡ��C
���� �����������е��龰Ϊģ�ͣ�����Ӧ��ţ�ٵڶ����ɽ����������������Ĺؼ���������˶�����Ϊ�ȼ��ٺ���٣�ͬʱ��ȷƽ���ٶȵļ��㷽����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ��С���Ҷ���һ��Բ�ι⻬���BC���г�������B�㣬һ������Ϊm=1.0kg��������Ϊ�ʵ����������A�㣬��С��һ�����ٶ�v0=5.0m/s�ع⻬ˮƽ�����������˶�������ϵ���ϴ�����ʵ��ɹ̶����Ҳ���ֱ�����ϣ���С��ѹ�����ɵ����ʱ������������������ѹ��Ҳ���ָ��α䣩����ʱ�����ǡ����С����B�����˺����ǡ����Բ������˶�����ߵ�C����֪С���ϱ���ˮƽ�������ĸ߶�h=0.45m��С��������ΪM=1.0kg��С���ij���Ϊl=1.0m����Բ�ι���뾶ΪR=0.4m�������С��֮��Ķ�Ħ������Ϊ��=0.2���������ٶ�gȡ10m/s2������
��ͼ��ʾ��С���Ҷ���һ��Բ�ι⻬���BC���г�������B�㣬һ������Ϊm=1.0kg��������Ϊ�ʵ����������A�㣬��С��һ�����ٶ�v0=5.0m/s�ع⻬ˮƽ�����������˶�������ϵ���ϴ�����ʵ��ɹ̶����Ҳ���ֱ�����ϣ���С��ѹ�����ɵ����ʱ������������������ѹ��Ҳ���ָ��α䣩����ʱ�����ǡ����С����B�����˺����ǡ����Բ������˶�����ߵ�C����֪С���ϱ���ˮƽ�������ĸ߶�h=0.45m��С��������ΪM=1.0kg��С���ij���Ϊl=1.0m����Բ�ι���뾶ΪR=0.4m�������С��֮��Ķ�Ħ������Ϊ��=0.2���������ٶ�gȡ10m/s2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ���������գ�
���������գ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 59W | B�� | 50W | C�� | 40W | D�� | 45W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 45 J | B�� | 75 J | C�� | 80 J | D�� | 85 J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �η�ʱ���������ӵ��˶� | |
| B�� | �������������ʱ���۾�ֱ�ӿ����Ŀ����г������˶� | |
| C�� | ������ˮ�е������˶� | |
| D�� | ϡ���˵�ī֭�е�С̿�����˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��Ϊԭ�Ӻ˺�С������ԭ�Ӻ�һ�����Ե����ʵ� | |
| B�� | �о��۲���ʳʱ������̫�������ʵ� | |
| C�� | �о�ƹ������תʱ���ɰ�ƹ�������ʵ� | |
| D�� | �о����϶����š��������ת������ʱ���ɰѡ��϶����š������ʵ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ľ�����ٶȱ�� | B�� | �ӵ�����ľ����ٶȱ�� | ||
| C�� | �ӵ��䴩ľ���ʱ��䳤 | D�� | ľ�����λ�Ʊ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
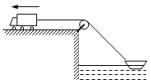 ��ͼ��ʾ�������ڰ����������������������н��ٶ�Ϊv������������ˮƽ����н�Ϊ$\frac{��}{6}$�����ٶ�Ϊ��������
��ͼ��ʾ�������ڰ����������������������н��ٶ�Ϊv������������ˮƽ����н�Ϊ$\frac{��}{6}$�����ٶ�Ϊ��������| A�� | $\frac{{\sqrt{3}}}{3}v$ | B�� | $\sqrt{3}v$ | C�� | $\frac{2}{3}\sqrt{3}v$ | D�� | $\frac{{\sqrt{3}}}{2}v$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com