
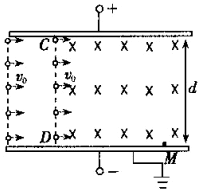
 空气中的颗粒物对人体健康有重要影响.有人利用除尘器对空气除尘,除尘器主要由过滤器、离子发生器(使颗粒物带电)、集尘器组成.如图所示为集尘器的截面 图,间距为d的上、下两板与直流电源相连,CD为匀强磁场的左边界,磁场的方向垂直纸面向里.质量均为m、带相等电荷量分布均匀的颗粒物,以水平速度v0进入集尘器,调节电源电压至U,颗粒物在电场区域恰能沿水平向右做匀速直线运动,再进入电场、磁场共存区域后颗粒物偏转碰到下板后其电量消失,同时被收集,设重力加速度为g,不计颗粒物之间的相互作用.
空气中的颗粒物对人体健康有重要影响.有人利用除尘器对空气除尘,除尘器主要由过滤器、离子发生器(使颗粒物带电)、集尘器组成.如图所示为集尘器的截面 图,间距为d的上、下两板与直流电源相连,CD为匀强磁场的左边界,磁场的方向垂直纸面向里.质量均为m、带相等电荷量分布均匀的颗粒物,以水平速度v0进入集尘器,调节电源电压至U,颗粒物在电场区域恰能沿水平向右做匀速直线运动,再进入电场、磁场共存区域后颗粒物偏转碰到下板后其电量消失,同时被收集,设重力加速度为g,不计颗粒物之间的相互作用.分析 (1)颗粒物在复合场中做匀速直线运动,重力等于电场力,写出平衡方程,即可判断出颗粒物的电性,并求出电量;
(2)颗粒垂直进入电、磁场共存的区域,重力仍然与电场力平衡,合力等于洛伦兹力,颗粒物做匀速圆周运动,由洛伦兹力提供向心力,写出动力学方程;结合轨迹中的几何关系即可求得磁感应强度;
(3)确定颗粒物运动的圆心,画出运动的轨迹,由几何关系求出半径与d的关系,然后结合洛伦兹力提供向心力,即可求得结果.
解答 解:(1)颗粒在电场中做匀速直线运动,有:q$\frac{U}{d}$=mg,解得:q=$\frac{mgd}{U}$,
由于电场的方向向下,电荷受到的电场力方向向上,可知颗粒带负电;
(2)颗粒垂直进入电、磁场共存的区域,重力仍然与电场力平衡,合力等于洛伦兹力,颗粒物做匀速圆周运动,
由牛顿第二定律得:qv0B1=m$\frac{{v}_{0}^{2}}{{R}_{1}}$,
由几何关系可知颗粒物在该区域恰好完成$\frac{1}{4}$圆周运动,则半径:R1=d,
解得:B1=$\frac{{v}_{0}U}{g{d}^{2}}$;
(3)确定圆心O1如图,由几何关系可得:
R2+R2sin30°=d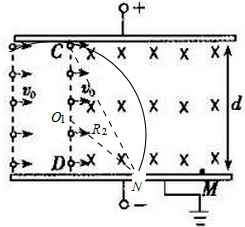
匀速圆周运动的半径为:R2=$\frac{2}{3}$d,
由牛顿第二定律得:qv0B2=m$\frac{{v}_{0}^{2}}{{R}_{2}}$,
解得:B2=$\frac{3{v}_{0}U}{2g{d}^{2}}$,
由上式决定的磁感应强度的大小与方向,可知从C点射入的粒子在N点射出的轨迹是所求磁场的一个边界.
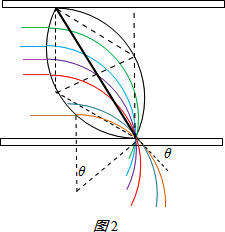
为确定另一个边界,我们采用逆向思维的方法,做出从N点射出的与下极板之间的夹角是θ的粒子运动的轨迹如图2,
则该磁场的左侧的边界也是一段圆弧,与过C到达N点的圆环具有对称性:
所求匀强磁场区域的最小面积如图中两个边界之间的部分,
为:S=2($\frac{1}{3}$πR22-$\frac{\sqrt{3}{R}_{2}^{2}}{4}$)=$\frac{(8π-6\sqrt{3}){d}^{2}}{27}$.
答:(1)颗粒物带负电荷,其电荷量q为$\frac{mgd}{U}$;
(2)磁感应强度B1的大小为$\frac{{v}_{0}U}{g{d}^{2}}$;
(3)此区域磁感应强度B2的大小为$\frac{3{v}_{0}U}{2g{d}^{2}}$,匀强磁场区域的最小面积S为$\frac{(8π-6\sqrt{3}){d}^{2}}{27}$.
点评 本题考查了带电粒子在电磁场中的运动,该题中判断出重力与电场力大小相等,方向相反,在存在磁场的区域中,颗粒物受到的合力等于洛伦兹力,并由洛伦兹力提供向心力,是解题的关键,常规题目,要注意按照规范化的解题步骤解题.


科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
| 实验次数 | 条数 | 速度m/s | 速度平方m2/s2 |
| 1 | 1 | 1.28 | 1.64 |
| 2 | 2 | 1.75 | 3.06 |
| 3 | 3 | 2.10 | 4.41 |
| 4 | 4 | 2.26 | 5.11 |
| 5 | 5 | 2.68 | 7.18 |
| 6 | 6 | 2.96 | 8.76 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
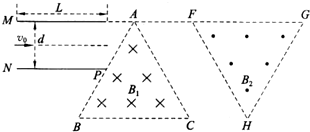
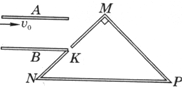 如图所示,水平放置的平行金属板A和B的间距为d,极板长为2d;金属板右侧有三块挡板MN,NP,PM围成一个等腰直角三角形区域,顶角∠NMP=90°,MN挡板上的中点处有一个小孔K恰好位于B板右端,已知水平挡板NP的长度为$\overline{NP}$=2$\sqrt{2}$a.由质量为m、带电量为+q的同种粒子组成的粒子束,以速度v0从金属板A、B左端沿板A射人,不计粒子所受的重力,若在A、B板间加一恒定电压,使粒子穿过金属板后恰好打到小孔K.求:
如图所示,水平放置的平行金属板A和B的间距为d,极板长为2d;金属板右侧有三块挡板MN,NP,PM围成一个等腰直角三角形区域,顶角∠NMP=90°,MN挡板上的中点处有一个小孔K恰好位于B板右端,已知水平挡板NP的长度为$\overline{NP}$=2$\sqrt{2}$a.由质量为m、带电量为+q的同种粒子组成的粒子束,以速度v0从金属板A、B左端沿板A射人,不计粒子所受的重力,若在A、B板间加一恒定电压,使粒子穿过金属板后恰好打到小孔K.求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
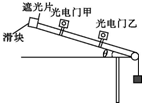 现要用如图所示的实验装置探究“动能定理”:一倾角θ可调的斜面上安装有两个光电门,其中光电门乙固定在斜面上,光电门甲的位置可移动.不可伸长的细线一端固定在带有遮光片(宽度为d)的滑块上,另一端通过光滑定滑轮与重物相连,细线与斜面平行(通过滑轮调节).当滑块沿斜面下滑时,与光电门相连的计时器可以显示遮光片挡光的时间t,从而可测出滑块通过光电门时的瞬时速度v.改变光电门甲的位置,重复实验,比较外力所做的功W与系统动能的增量△Ek的关系,即可达到实验目的.
现要用如图所示的实验装置探究“动能定理”:一倾角θ可调的斜面上安装有两个光电门,其中光电门乙固定在斜面上,光电门甲的位置可移动.不可伸长的细线一端固定在带有遮光片(宽度为d)的滑块上,另一端通过光滑定滑轮与重物相连,细线与斜面平行(通过滑轮调节).当滑块沿斜面下滑时,与光电门相连的计时器可以显示遮光片挡光的时间t,从而可测出滑块通过光电门时的瞬时速度v.改变光电门甲的位置,重复实验,比较外力所做的功W与系统动能的增量△Ek的关系,即可达到实验目的.查看答案和解析>>
科目:高中物理 来源: 题型:作图题
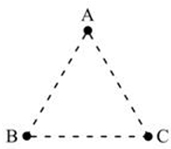 如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形平面.已知φA=2V,φB=8V,φC=4V.用作图法,请在图中画出过C点的等势面和过A点的电场线.
如图所示,在匀强电场中有一个等边三角形ABC,且电场线平行于该三角形平面.已知φA=2V,φB=8V,φC=4V.用作图法,请在图中画出过C点的等势面和过A点的电场线.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
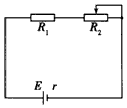 如图所示,已知电源的电动势E=5V,内阻r=2Ω,定值电阻R1=0.5Ω,滑动变阻器R2的最大阻值为10Ω.求:
如图所示,已知电源的电动势E=5V,内阻r=2Ω,定值电阻R1=0.5Ω,滑动变阻器R2的最大阻值为10Ω.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com