

分析 根据连续相等时间内的位移之差是一恒量求出重力加速度g的表达式,根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点3的瞬时速度.从而结合速度时间公式求出计数点5的瞬时速度.
解答 解:根据${s}_{4}-{s}_{1}=3g{T}^{2}$,则g=$\frac{{s}_{4}-{s}_{1}}{3{T}^{2}}=\frac{({s}_{4}-{s}_{1}){f}^{2}}{3}$.
计数点3的瞬时速度${v}_{3}=\frac{{s}_{3}+{s}_{4}}{2T}=\frac{({s}_{3}+{s}_{4})f}{2}$,加速度a=$\frac{{s}_{4}-{s}_{3}}{{T}^{2}}=({s}_{4}-{s}_{3}){f}^{2}$,
则计数点5的瞬时速度v5=v3+2aT=$\frac{({s}_{3}+{s}_{4})f}{2}+2({s}_{4}-{s}_{3})f$=$\frac{(5{s}_{4}-3{s}_{3})f}{2}$.
故答案为:$\frac{({s}_{4}-{s}_{1}){f}^{2}}{3}$,$\frac{(5{s}_{4}-3{s}_{3})f}{2}$.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.


科目:高中物理 来源: 题型:解答题
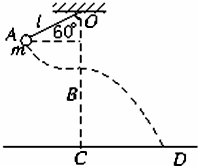 如图所示,质量m=2kg的摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时刚好线被拉断.设摆线长L=1.6m,悬点O到地面C的竖直高度为H=6.6m,不计空气阻力,g=10m/s2,求:
如图所示,质量m=2kg的摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时刚好线被拉断.设摆线长L=1.6m,悬点O到地面C的竖直高度为H=6.6m,不计空气阻力,g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 重力就是地球对物体的吸引力 | |
| B. | 只有静止的物体才受到重力 | |
| C. | 同一物体在地球上无论怎样运动都受到重力 | |
| D. | 重力的方向总是垂直向下的 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{s}_{1}}{{s}_{2}}$=$\frac{{t}_{2}}{{t}_{1}}$ | B. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{t}_{1}}{{t}_{2}}$ | ||
| C. | $\frac{{s}_{1}}{{t}_{1}}$=$\frac{{s}_{2}}{{t}_{2}}$=v | D. | v=$\frac{{2({s_1}+{s_2})}}{{{t_1}+{t_2}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一小球在光滑的V形槽中,由A点释放经B点到达与A点等高的C点.设A点的高度为1m,则下列说法中正确的是( )
如图所示,一小球在光滑的V形槽中,由A点释放经B点到达与A点等高的C点.设A点的高度为1m,则下列说法中正确的是( )| A. | 在全过程中小球通过的位移和路程分别为1m和$\frac{4}{3}$$\sqrt{3}$m | |
| B. | 在由A到B的过程中,小球通过的位移和路程分别为$\frac{2}{3}$$\sqrt{3}$m和$\frac{2}{3}$$\sqrt{3}$m | |
| C. | 在全过程中,小球通过的位移和路程分别为$\frac{2}{3}$$\sqrt{3}$ m和$\frac{4}{3}$$\sqrt{3}$m | |
| D. | 在由A到C的过程中,小球通过的位移和路程分别为1m、1m |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
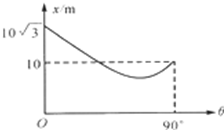 物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,下列说法正确的是( )
物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,下列说法正确的是( )| A. | 物体与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$ | B. | 物体与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{2}$ | ||
| C. | 当θ=30°时,x有最小值xmin=5$\sqrt{3}$m | D. | 当θ=60°时,x有最小值xmin=5$\sqrt{3}$m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
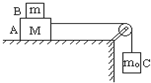 如图,A、B、C三物体质量分别为M、m、m0,绳子不可伸长,且绳子和滑轮的摩擦均不计,若B随A一起沿水平桌面向右做匀速运动,则可以断定( )
如图,A、B、C三物体质量分别为M、m、m0,绳子不可伸长,且绳子和滑轮的摩擦均不计,若B随A一起沿水平桌面向右做匀速运动,则可以断定( )| A. | 物体A与桌面之间有摩擦力,大小为m0g | |
| B. | 物体A与B之间有摩擦力,大小为μmg | |
| C. | 桌面对A,B对A,都有摩擦力,两者方向相同,大小均为m0g | |
| D. | 桌面对A,B对A,都有摩擦力,两者方向相反,大小均为m0g |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com