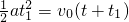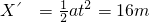一辆值勤的警车停在公路边,当警员发现从他旁边以v=8m/s的速度匀速行驶的货车有违章行为时,决定前去追赶,经2.5s警车发动起来,以加速度a=2m/s2 做匀加速运动.试问:
(1)警车要多长时间才能追上违章的货车?
(2)在警车追上货车之前,两车间的最大距离是多少?
解:(1)当警车追上货车时,二者位移相等,由此有
X
2=X
0+X
1
即
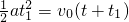
带入数据有:t
12-8t
1-20=0,解得t
1=10s,t
2=-2s(舍)
故警车要10s时间才能追上违章的货车.
(2)当v
车=v
货时相距最远,此时有:
v
车=v
货=at
2,解得:t
2=4s;
此时货车X=v
0(t
0+t
2)=52m
警车
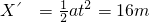
最大距离 X
m=X-X'=36m
故在警车追上货车之前,两车间的最大距离是36m.
分析:(1)警车追上货车时,两车的路程相等,由此列方程可以求出警车追上货车的时间,注意警车在发动时间内,货车做匀速运动;
(2)刚开始货车的速度大于警车速度,故两车之间的距离越来越大,当两车速度相等时,位移最大;分别求出两车的路程,然后求出两车间的最大距离.
点评:两物体在同一直线上运动,往往涉及到追击、相遇或避免碰撞等问题,解答此类问题的关键是找出时间关系、速度关系、位移关系,注意两者速度相等时,往往是能否追上或者二者之间有最大或者最小值的临界条件.