
 ��ͼ��ʾ�����е������ֵ��ƽ�н�����M��N��ֱ���ã�M��N�����ľ���d=0.5m���ֽ�һ����m=1��10-2kg�������q=4��10-5C�Ĵ���С����������Ϸ���A����v0=4m/s�ij��ٶ�ˮƽ�׳���A����������϶˵ĸ߶�h=0.2m��֮��С��ǡ�ôӿ���M���϶˴���������䣬��ֱ���˶�����N���ϵ�C�㣬��ֱ�������ߵ�ĩ�����У�����ǿ�糡ֻ������M��N֮�䣬���ƿ���������ȡg=10m/s2����
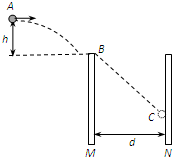
��ͼ��ʾ�����е������ֵ��ƽ�н�����M��N��ֱ���ã�M��N�����ľ���d=0.5m���ֽ�һ����m=1��10-2kg�������q=4��10-5C�Ĵ���С����������Ϸ���A����v0=4m/s�ij��ٶ�ˮƽ�׳���A����������϶˵ĸ߶�h=0.2m��֮��С��ǡ�ôӿ���M���϶˴���������䣬��ֱ���˶�����N���ϵ�C�㣬��ֱ�������ߵ�ĩ�����У�����ǿ�糡ֻ������M��N֮�䣬���ƿ���������ȡg=10m/s2�������� ��1������ƽ���˶��Ļ�����ʽ���С��ս���糡ʱ��ֱ������ٶȴ�С�ͷ���
��2��С���ڵ糡����ֱ���˶���������ֱ�߷��������ĺϳ�����糡���������Ĺ�ϵ��������õ糡ǿ�ȵĴ�С�ͷ���
��3����A��B�Ĺ��������ö��ܶ���������⣮Ҳ���������˶��ĺϳɷ����
��� �⣺��1��С��ƽ���˶�����ˮƽ����������ֱ���˶���vx=v0=4 m/s
��ֱ�������ȼ�����ֱ���˶���$h=\frac{1}{2}g{t_1}^2$��vy=gt1=2 m/s
�ý⣺${v_B}=\sqrt{v_x^2+v_y^2}=2\sqrt{5}$m/s
���� $tan��=\frac{v_y}{v_x}=\frac{1}{2}$����=arctan0.5����Ϊ�ٶȷ�����ˮƽ����ļнǣ�
��2��С�����糡����ֱ���˶���C�㣬����������糡���ĺ������ظ�ֱ�߷���
�� $tan��=\frac{mg}{qE}=\frac{1}{2}$
�ý⣺$E=\frac{2mg}{q}=5��{10^3}$N/C������ˮƽ���ң�
��3���ⷨһ��
����糡��С���ܵ��ĺ�����${F_��}=\sqrt{��mg{��^2}+{{��qE��}^2}}=\sqrt{5}mg$
B��C�����ľ���$s=\frac{d}{cos��}$��$cos��=\frac{2}{{\sqrt{5}}}$
��B��C�ɶ��ܶ����ã�${F_��}s={E_{kC}}-\frac{1}{2}mv_B^2$
��ã�EkC=0.225J
�ⷨ��������糡��С����ˮƽ���������ٶ�Ϊv0���ȼ���ֱ���˶�$d={v_0}{t_2}+\frac{1}{2}a{t_2}^2$��${a_x}=\frac{qE}{m}=20$m/s2
�ý⣺t2=0.1 s
С��C��ʱ��ˮƽ�ٶ�v1=v0+axt2=6 m/s
��ֱ���ٶ�v2=vy+gt2=3 m/s
vC=$\sqrt{v_1^2+v_2^2}$
EkC=$\frac{1}{2}mv_c^2$=$\frac{1}{2}m��v_1^2+v_2^2��$=0.225 J
��
��1��С��M�����ϱ�ԵBλ��ʱ�ٶȵĴ�С��2$\sqrt{5}$m/s��������ˮƽ����ļн�Ϊarctan0.5��
��2��M��N�����ĵ糡ǿ�ȵĴ�С��5��103N/C������ˮƽ���ң�
��3��С��C��ʱ�Ķ�����0.225 J��
���� �������Ĺؼ�֪��ƽ���˶��Ĺ��ɣ��Լ�֪��С�����糡���ٶȷ�����С�����ܵĺ���������ͬ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����������Ƶ�ʣ������ݳ������� | |
| B�� | ֻ�ӳ����������ʱ�䣬�����й���Ӵӽ��������ݳ� | |
| C�� | ����������Ƶ�ʣ����ܻ��й���Ӵӽ��������ݳ� | |
| D�� | ����������Ƶ�ʣ�һ�����й���Ӵӽ��������ݳ� | |
| E�� | ֻ����������ǿ�ȣ�����Ӵӽ��������ݳ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
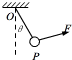 ��ͼ��ʾ��������Ϊm��С��P��ϸ��������O�㣬������F��סС��Pʹ�䴦�ھ�ֹ״̬��Ҫ����������ֱ����ɦ�=30��ǣ�����F����СֵΪ��������
��ͼ��ʾ��������Ϊm��С��P��ϸ��������O�㣬������F��סС��Pʹ�䴦�ھ�ֹ״̬��Ҫ����������ֱ����ɦ�=30��ǣ�����F����СֵΪ��������| A�� | $\frac{\sqrt{3}}{2}$mg | B�� | $\frac{1}{2}$mg | C�� | $\frac{\sqrt{3}}{2}$mg | D�� | mg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
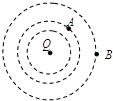 ��ͼ���ڵ���Q�����ĵ糡�У����������������̽���q1��q2�ֱ�����A��B���㣬����Ϊ�����ߣ�ȡ����Զ��Ϊ����Ƶ㣬����q1��q2�ƶ�������Զ�Ĺ����������˷��糡�����Ĺ���ȣ�������˵����ȷ���ǣ�������
��ͼ���ڵ���Q�����ĵ糡�У����������������̽���q1��q2�ֱ�����A��B���㣬����Ϊ�����ߣ�ȡ����Զ��Ϊ����Ƶ㣬����q1��q2�ƶ�������Զ�Ĺ����������˷��糡�����Ĺ���ȣ�������˵����ȷ���ǣ�������| A�� | A����Ƹ���B����� | |
| B�� | A��B����ĵ糡ǿ����� | |
| C�� | q1�ĵ����С��q2�ĵ���� | |
| D�� | q1��A��ĵ�����С��q2��B��ĵ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾΪijһ����Q�����ĵ糡�е�һ���糡�ߣ�A��B��һ���糡���ϵ����㣬����A���ͷ�һ����Ϊ��ĵ��ӣ����ӽ��ܵ糡�����ã��ص糡�ߴ�A�˶���B��������
��ͼ��ʾΪijһ����Q�����ĵ糡�е�һ���糡�ߣ�A��B��һ���糡���ϵ����㣬����A���ͷ�һ����Ϊ��ĵ��ӣ����ӽ��ܵ糡�����ã��ص糡�ߴ�A�˶���B��������| A�� | �糡�߷�����Bָ��A | B�� | A�㳡ǿһ������B�㳡ǿ | ||
| C�� | ��QΪ����ɣ���Q��A����� | D�� | ��A�˶���B�����ӵ��������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
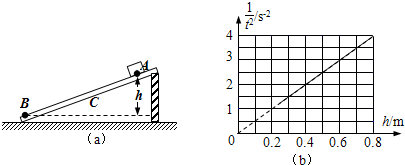
 ��ͼ���㹻��Ĺ⻬��Եˮƽ���������������ʵ㣬A��CΧ��B������Բ���˶���Bǡ�ܱ��־�ֹ������A��C��B�ľ���ֱ���L1����L2���������ʵ���������������A��C�ıȺɣ�����������֮�ȣ�֮��Ӧ�ǣ�������
��ͼ���㹻��Ĺ⻬��Եˮƽ���������������ʵ㣬A��CΧ��B������Բ���˶���Bǡ�ܱ��־�ֹ������A��C��B�ľ���ֱ���L1����L2���������ʵ���������������A��C�ıȺɣ�����������֮�ȣ�֮��Ӧ�ǣ�������| A�� | ��$\frac{{L}_{1}}{{L}_{2}}$��2 | B�� | ��$\frac{{L}_{1}}{{L}_{2}}$��3 | C�� | ��$\frac{{L}_{2}}{{L}_{1}}$��2 | D�� | ��$\frac{{L}_{2}}{{L}_{1}}$��3 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
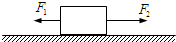 ��ͼ��ʾ������ˮƽ��������壬�ܵ�ˮƽ�����F1=15N��ˮƽ���ҵ�F2=30N�������Ĺ�ͬ���ö���ֹ���ֳ�ȥ��F2���������ܵ���Ħ������С�ͷ���Ϊ��������
��ͼ��ʾ������ˮƽ��������壬�ܵ�ˮƽ�����F1=15N��ˮƽ���ҵ�F2=30N�������Ĺ�ͬ���ö���ֹ���ֳ�ȥ��F2���������ܵ���Ħ������С�ͷ���Ϊ��������| A�� | 15N��ˮƽ���� | B�� | 15N��ˮƽ���� | C�� | 30N��ˮƽ���� | D�� | 30N��ˮƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
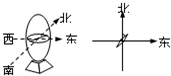 ��֪�شų���ˮƽ����ΪB��������һֵ���Բⶨijһ���ų��ĴŸ�ǿ�ȣ���ͼ��ʾΪ�ⶨͨ����Ȧ����һ��ĴŸ�ǿ�ȣ�ʵ�鷽����
��֪�شų���ˮƽ����ΪB��������һֵ���Բⶨijһ���ų��ĴŸ�ǿ�ȣ���ͼ��ʾΪ�ⶨͨ����Ȧ����һ��ĴŸ�ǿ�ȣ�ʵ�鷽�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com