
| A�� | �ɴ����ٶ�����������Բ���˶�������ٶ� | |
| B�� | �����ǵ�ƽ���ܶȿɱ�ʾΪ$\frac{3��}{4GT^2}$ | |
| C�� | �����ǵ�ƽ���ܶȿɱ�ʾΪ$\frac{3g}{4��GR}$ | |
| D�� | �ɴ���Բ���˶��İ뾶�������˶����ڽ���С |
���� ���ݷɴ��ܵ��������������ڷɴ���Ҫ�����������Լ����������������������������������ʽ��⣻
��� �⣺A���ɴ������Ǹ���������Բ���˶�
$G\frac{M{m}^{��}��}{{R}^{2}}={m}^{��}��\frac{{v}^{2}}{R}$
���
$v=\sqrt{\frac{GM}{R}}$���ɴ����ٶ��滷�ư뾶���������С����֪�ɴ��Ĺ���뾶����Ϊ�����ǰ뾶Rʱ���ɴ����ٶ�����������Բ���˶�������ٶȣ���A��ȷ��
B�����ǶԷɴ������������ṩ�ɴ�����������
$G\frac{Mm}{r^2}=m{��\frac{2��}{T}��^2}r$
���
$M=\frac{4{��}^{2}{r}^{3}}{G{T}^{2}}$
�֣�M=��V=$��•\frac{4}{3}��{R}^{3}$
���Ը����ǵ�ƽ���ܶȿɱ�ʾΪ$��=\frac{M}{V}=\frac{\frac{4{��}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4��{R}^{3}}{3}}=\frac{3��}{G{T}^{2}}$����B����
C������������������
$m��g=\frac{GMm��}{{R}^{2}}$
��ã�M=$\frac{g{R}^{2}}{G}$
���Ը����ǵ�ƽ���ܶȿɱ�ʾΪ��$��=\frac{M}{V}=\frac{\frac{g{R}^{2}}{G}}{\frac{4��{R}^{3}}{3}}=\frac{3g}{4��GR}$����C��ȷ��
D�����ǶԷɴ������������ṩ�ɴ�����������
$G\frac{Mm}{r^2}=m{��\frac{2��}{T}��^2}r$
��ã�T=$2��\sqrt{\frac{{r}^{3}}{GM}}$����֪�ɴ���Բ���˶��İ뾶�������˶����ڽ�����D����
��ѡ��AC
���� ���⿼�������������ɵ�һ��Ӧ�ã������ؼ�ץס��������������������������ɴ�����������������������


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д� �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
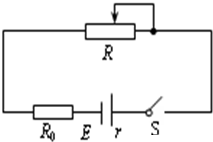 ��ͼ��ʾ����Դ�ĵ綯��Ϊ6v������Ϊ0.5����R0Ϊ1.5����RΪ����ֵΪ10���Ļ���������������������������������ʱ����������ֵӦ��������������
��ͼ��ʾ����Դ�ĵ綯��Ϊ6v������Ϊ0.5����R0Ϊ1.5����RΪ����ֵΪ10���Ļ���������������������������������ʱ����������ֵӦ��������������| A�� | 0�� | B�� | 0.5�� | C�� | 2�� | D�� | 10�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
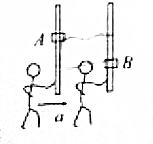
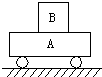 ��ͼ��ʾ��С��A�Ϸ�һľ��B���� A��B��Ծ�ֹ����С���������˶�ʱ����B�����������������ȷ���ǣ�������
��ͼ��ʾ��С��A�Ϸ�һľ��B���� A��B��Ծ�ֹ����С���������˶�ʱ����B�����������������ȷ���ǣ�������| A�� | ������֧������ѹ�� | B�� | ������֧������Ħ���� | ||
| C�� | ������֧���� | D�� | ������֧������ѹ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
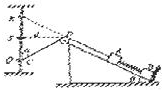 ��ͼ��ʾ����Ǧ�=37��Ĺ⻬���㹻����б��̶���ˮƽ���ϣ���б�涥�˹̶�һ���ְ뾶���������ƵĹ⻬������ D��������Ϊm=1kg������A��B��һ����ϵ��k=240N/m���ᵯ�����ӣ�����B��λ��б����Ҵ�ֱ��б��ĵ���P��ס����һ�����쳤������ʹ����A���������������ΪM��С��C���ӣ�С��C������ֱ�̶��Ĺ⻬����ϸ�ˣ�������ϵͳ��ֹʱ����Cλ��Q��������ϸ�˵ļнǦ�=53�㣬������B�Ե���P��ѹ��ǡ��Ϊ�㣬ͼ��SDˮƽ�ҳ���Ϊ d=0.2m��λ��R��λ��Q����λ��S�Գƣ��ᵯ�ɺͶ������Ҳ��������б��ƽ�У����û�C��λ��R�ɾ�ֹ�ͷţ�sin37��=0.6��cos37��=0.8��g ȡ 10m/s2����
��ͼ��ʾ����Ǧ�=37��Ĺ⻬���㹻����б��̶���ˮƽ���ϣ���б�涥�˹̶�һ���ְ뾶���������ƵĹ⻬������ D��������Ϊm=1kg������A��B��һ����ϵ��k=240N/m���ᵯ�����ӣ�����B��λ��б����Ҵ�ֱ��б��ĵ���P��ס����һ�����쳤������ʹ����A���������������ΪM��С��C���ӣ�С��C������ֱ�̶��Ĺ⻬����ϸ�ˣ�������ϵͳ��ֹʱ����Cλ��Q��������ϸ�˵ļнǦ�=53�㣬������B�Ե���P��ѹ��ǡ��Ϊ�㣬ͼ��SDˮƽ�ҳ���Ϊ d=0.2m��λ��R��λ��Q����λ��S�Գƣ��ᵯ�ɺͶ������Ҳ��������б��ƽ�У����û�C��λ��R�ɾ�ֹ�ͷţ�sin37��=0.6��cos37��=0.8��g ȡ 10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
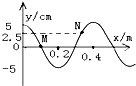 ��ͼΪһ�м�г����t1=0ʱ�̵�ͼ��ʱ�����ʵ�M���˶�������y�������ҵ�t2=0.5s�ʵ�Mǡ�õ�1�ε���y���������λ�ƴ�������
��ͼΪһ�м�г����t1=0ʱ�̵�ͼ��ʱ�����ʵ�M���˶�������y�������ҵ�t2=0.5s�ʵ�Mǡ�õ�1�ε���y���������λ�ƴ��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
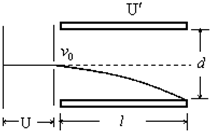 һ����������A�����м��С���ɾ�ֹ���벢��U=880V�ļ��ٵ�ѹ���ٺ�B�����м��С�����ٶ�v0�ɳ�������������Ⱦദ��ֱ����ƽ�а�C��D�����ǿ�糡����ͼ��ʾ����������d=1.0cm���峤l=5cm����֪���ӵĵ�������������ı�ֵ��e/m��=1.76��1011C/kg�������´𰸳������ģ�����ȡ�������Ƶ�������Ӱ�죩
һ����������A�����м��С���ɾ�ֹ���벢��U=880V�ļ��ٵ�ѹ���ٺ�B�����м��С�����ٶ�v0�ɳ�������������Ⱦദ��ֱ����ƽ�а�C��D�����ǿ�糡����ͼ��ʾ����������d=1.0cm���峤l=5cm����֪���ӵĵ�������������ı�ֵ��e/m��=1.76��1011C/kg�������´𰸳������ģ�����ȡ�������Ƶ�������Ӱ�죩�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 �ڡ���֤ţ�ٵڶ����ɡ���ʵ���У��ס�������ͬѧ�ֱ𰴲�������ʵ��ʱ�����Եõ�����ͼ������ʾ��ͼ������ִ��������ԭ��
�ڡ���֤ţ�ٵڶ����ɡ���ʵ���У��ס�������ͬѧ�ֱ𰴲�������ʵ��ʱ�����Եõ�����ͼ������ʾ��ͼ������ִ��������ԭ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��ijͬѧ��һ������Ϊm��С����������ֱ�⻬��ϸ���ϣ��������������»��龲ֹ��ϸ����A�㣮����ͬѧ����ϸ����ˮƽ�����ɾ�ֹ�����ٶȴ�СΪa���ȼ���ֱ���˶���ͬʱ��ȥ������С�����ϵ�����������ʱ��t��������λ��A�˶���λ��B���������ٶ�Ϊg��������˵����ȷ���ǣ�������
��ͼ��ʾ��ijͬѧ��һ������Ϊm��С����������ֱ�⻬��ϸ���ϣ��������������»��龲ֹ��ϸ����A�㣮����ͬѧ����ϸ����ˮƽ�����ɾ�ֹ�����ٶȴ�СΪa���ȼ���ֱ���˶���ͬʱ��ȥ������С�����ϵ�����������ʱ��t��������λ��A�˶���λ��B���������ٶ�Ϊg��������˵����ȷ���ǣ�������| A�� | С������A�˶���B�Ĺ켣Ϊ���� | |
| B�� | AB��ĸ߶Ȳ�Ϊ$\frac{1}{2}{at}^{2}$ | |
| C�� | AB��ľ���Ϊ$\frac{{t}^{2}}{2}\sqrt{{a}^{2}{+g}^{2}}$ | |
| D�� | С�����ٶ���ˮƽ����ļн������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com