
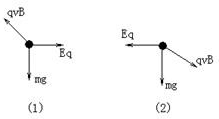
 如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B=0.5T,还有沿x轴负方向的匀强电场,场强大小为E=
如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B=0.5T,还有沿x轴负方向的匀强电场,场强大小为E=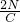 .在其第一象限空间有沿y轴负方向的、场强大小也为E的匀强电场,并在y>h=0.4m的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场.一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作匀速直线运动(PO与x轴负方向的夹角为θ=45°),并从原点O进入第一象限.已知重力加速度g=10m/s2,问:
.在其第一象限空间有沿y轴负方向的、场强大小也为E的匀强电场,并在y>h=0.4m的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场.一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作匀速直线运动(PO与x轴负方向的夹角为θ=45°),并从原点O进入第一象限.已知重力加速度g=10m/s2,问:


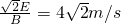
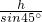 =
= 知运动时间:t
知运动时间:t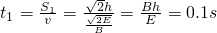
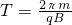 知由A→C的圆周运动时间为
知由A→C的圆周运动时间为 =
= ,由对称性知从C→N的时间t2=t3
,由对称性知从C→N的时间t2=t3
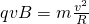 ,解得轨道半径
,解得轨道半径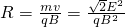
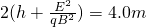


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
 如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A点距地面高度为H,质量为m的小球从A点静止释放(球达B点水平速度大小等于球由O点自由释放至B点速度大小),最后落在地面C处,不计空气阻力,( g=10m/s2)求:
如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A点距地面高度为H,质量为m的小球从A点静止释放(球达B点水平速度大小等于球由O点自由释放至B点速度大小),最后落在地面C处,不计空气阻力,( g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A距地面高度为H,质量为m的小球从A静止释放,最后落在地面C点处,不计空气阻力.求:
如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A距地面高度为H,质量为m的小球从A静止释放,最后落在地面C点处,不计空气阻力.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,位于竖直平面上的
如图所示,位于竖直平面上的| 1 |
| 4 |
| 2gR |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点由静止释放,最后落在地面上C点处,不计空气阻力,求:
如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点由静止释放,最后落在地面上C点处,不计空气阻力,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,位于竖直平面上的
如图所示,位于竖直平面上的| 1 |
| 4 |
| R |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com