
 ��ͼ��ʾ�������ѹ��ԭ������Ȧ������n1��n2=1��2��ԭ��Ȧ�ӵ�ѹ��ʱ��仯����Ϊu=220$\sqrt{2}$sin100��t��V���Ľ�����Դ��A1��A2��A3�����������������DΪ��������ܣ�R1�ǻ�������������ֵ����R2=R3=220����������
��ͼ��ʾ�������ѹ��ԭ������Ȧ������n1��n2=1��2��ԭ��Ȧ�ӵ�ѹ��ʱ��仯����Ϊu=220$\sqrt{2}$sin100��t��V���Ľ�����Դ��A1��A2��A3�����������������DΪ��������ܣ�R1�ǻ�������������ֵ����R2=R3=220����������| A�� | ������A2��Ϊ1.0A | |
| B�� | ������A2��Ϊ2.0A | |
| C�� | ����������R1�Ļ�Ƭ���»���ʱ��������A1�Ľ���� | |
| D�� | ����������R1�Ļ�Ƭ���ϻ���ʱ����ѹ�����빦������ |
���� ���ݱ���ʽ������������ѹ����Чֵ�����ں�Ƶ�ʵȣ������ܵ�������ֻ��������ĵ���ͨ�����ٸ��ݵ�ѹ�����������ȼ�����ý��ۣ�
��� �⣺ԭ��Ȧ�ӵ�ѹ��ʱ��仯����Ϊu=220$\sqrt{2}$sin100��t��V���������ֵ��220$\sqrt{2}$V����ЧֵΪ��
${U}_{1}^{\;}=\frac{{U}_{m}^{\;}}{\sqrt{2}}=\frac{220\sqrt{2}}{\sqrt{2}}V=220V$
����Ȧ���˵ĵ�ѹΪ��${U}_{2}^{\;}=\frac{{n}_{2}^{\;}}{{n}_{1}^{\;}}{U}_{1}^{\;}=\frac{2}{1}��220V=440V$
A�����ڵ���R2��һ��������������ֻ��һ���ʱ�����е���ͨ���������ѹ����ЧֵΪU�䣬���У�
$\frac{U{��}_{\;}^{2}}{R}•T=\frac{{U}_{2}^{2}}{R}•\frac{T}{2}$
���ԣ�U��=220$\sqrt{2}$V
����R2�ĵ���Ϊ��${I}_{2}^{\;}=\frac{U��}{{R}_{2}^{\;}}=\frac{220\sqrt{2}}{220}A=\sqrt{2}A$����A����
B��R3���˵ĵ�ѹ�Ǹ���Ȧ���˵ĵ�ѹ����440V����������R3�ĵ���Ϊ��${I}_{3}^{\;}=\frac{{U}_{2}^{\;}}{{R}_{3}^{\;}}=\frac{440}{220}A=2A$����B��ȷ��
C������������R1�Ļ�Ƭ���»�ʱ�������·�еĵ���ֵ��С����������R1�ĵ���ֵ�������Ը���Ȧ�е��ܵ���ֵ��������ԭ��Ȧ�еĵ���ֵҲ����������${A}_{1}^{\;}$��ʾ��������C��ȷ��
D������������R1�Ļ�Ƭ���ϻ�ʱ�������·�еĵ���ֵ������������R1�ĵ���ֵ��С�����Ը���Ȧ�е��ܵ���ֵ��С������Ȧ�еĸ������ĵ��ܹ��ʼ�С������ԭ��Ȧ��������ܹ��ʼ�С����D����
��ѡ��BC
���� �����϶����ܵĵ����Կ����ѹ���ĵ�ѹ֮�Ⱥ�������֮��Ĺ�ϵ���Լ����������Чֵ�ļ��㣬�������Ҫ���ձ�ѹ���ĵ�ѹ֮�Ⱥ�������֮��Ĺ�ϵ��ͬʱ���ڶ����ܺ͵�����������Ҫ�˽⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �������ӽ��ڵ糡�������£��ӵ糡��a���Գ��ٶ�vo����糡����������ʾ�Ĺ켣�˶���b�㣬��ͼ��ʾ�������жϣ�������
�������ӽ��ڵ糡�������£��ӵ糡��a���Գ��ٶ�vo����糡����������ʾ�Ĺ켣�˶���b�㣬��ͼ��ʾ�������жϣ�������| A�� | ���ӵļ��ٶ���a��ʱ�ϴ� | |
| B�� | ���ӵĵ�������b��ʱ��С | |
| C�� | ���ӿ��ܴ����磬��b��ʱ�ٶȽϴ� | |
| D�� | ����һ�������磬�����ȱ�С���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��������Ϊ˳ʱ�룬����ǿ��Ϊ$\frac{ve}{2��r}$ | |
| B�� | ��������Ϊ˳ʱ�룬����ǿ��Ϊ$\frac{ve}{r}$ | |
| C�� | ��������Ϊ��ʱ�룬����ǿ��Ϊ$\frac{ve}{2��r}$ | |
| D�� | ��������Ϊ��ʱ�룬����ǿ��Ϊ$\frac{ve}{r}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�ȼ����»�������B������ֲ�ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩���ȼ����˶����ͣ��C�㣮ÿ��0.2��ͨ���ٶȴ��������������˲ʱ�ٶȴ�С���������˲��ֲ������ݣ���
��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�ȼ����»�������B������ֲ�ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩���ȼ����˶����ͣ��C�㣮ÿ��0.2��ͨ���ٶȴ��������������˲ʱ�ٶȴ�С���������˲��ֲ������ݣ���| t/��s�� | 0.0 | 0.2 | 0.4 | �� | 1.2 | 1.4 | �� |
| V/��m/s�� | 0.0 | 1.0 | 2.0 | �� | 1.1 | 0.7 | �� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ1�ڴֲڵ�ˮƽ������һ��3kg�����壬��0��4s����ˮƽ������F�����ã���4��10s�ڳ�ȥˮƽ����F����v-tͼ����ͼ2��ʾ����
��ͼ1�ڴֲڵ�ˮƽ������һ��3kg�����壬��0��4s����ˮƽ������F�����ã���4��10s�ڳ�ȥˮƽ����F����v-tͼ����ͼ2��ʾ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��n����ͬ�������Ե��ٶ�v�ؿ�Ϊd��ֱ��·��ʻ��ÿ����Ϊb�����Ϊa������������С�ٶ���ֱ�ߴ�ֱ������·�������õ�ʱ��Ϊ��������
��ͼ��ʾ��n����ͬ�������Ե��ٶ�v�ؿ�Ϊd��ֱ��·��ʻ��ÿ����Ϊb�����Ϊa������������С�ٶ���ֱ�ߴ�ֱ������·�������õ�ʱ��Ϊ��������| A�� | $\frac{ad}{bv}$ | B�� | $\frac{ab}{dv}$ | ||
| C�� | $\frac{d��{a}^{2}+{b}^{2}��}{abv}$ | D�� | �������㣬����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | ���̶��˵�Ħ�����������ṩ����Բ���˶���������ʱ���˻���Զ��Բ�� | |
| B�� | ���̶��˵�Ħ�����������ṩ����Բ���˶���������ʱ���˻�����Բ�� | |
| C�� | ���ܵ���������������Ӧ�������Ŀ�£ | |
| D�� | ���ܵ���������������Ӧ�����Ե�˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
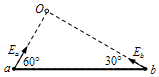 ��ͼ��ʾ�������O����һ���ɣ��ھ������ĵ糡����a��b���㣬a��ij�ǿ��СΪEa��������ab���߳�60��ǣ�b��ij�ǿ��СΪEb��������ab���߳�30��ǣ�����ͬһ��̽��ɷֱ����a��b�����ܵ糡����С�ֱ�ΪFa��Fb���������̽�����a��b����糡���Ĵ�С��ϵ�����½�����ȷ���ǣ�������
��ͼ��ʾ�������O����һ���ɣ��ھ������ĵ糡����a��b���㣬a��ij�ǿ��СΪEa��������ab���߳�60��ǣ�b��ij�ǿ��СΪEb��������ab���߳�30��ǣ�����ͬһ��̽��ɷֱ����a��b�����ܵ糡����С�ֱ�ΪFa��Fb���������̽�����a��b����糡���Ĵ�С��ϵ�����½�����ȷ���ǣ�������| A�� | Fa=3Fb | B�� | Fa=$\sqrt{3}$Fb | C�� | Fa=$\frac{\sqrt{3}}{3}$Fb | D�� | Fa=$\frac{1}{3}$Fb |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com