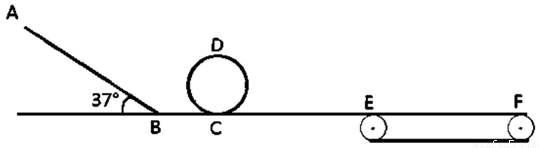解答:解:(1)物体由H处下落到达B端,由动能定理:mgH-μmgcos37°
?=
m代入数据解得:v
B=6m/s
物体运动到由B运动到D点:
-2mgR=mvD2-mvB2D点有:
N1+mg=m得:N
1=62.5N
(2)物体若能通过D点在水平面处的最小速度为v
0,则由动能定理:
-2mgR=m()2-mv02得:v
0=4m/s
物体上传送带时速度为6m/s,上传送带后先减速为0,再反向加速:5m/s<6m/s,则反向时E的速度为5m/s.由5m/s>4m/s,物体能够到达D点.
物体运动到由E运动到D点:
-2mgR=mvD2-mvE2D点有:
N2+mg=m得:N
2=28.125N
(3)物体运动若要第二次到达D点,从传送带上返回E点时,速度至少为4m/s,则传送带的速度至少为4m/s.
物体滑上传送带后的运动图象可由下图表示
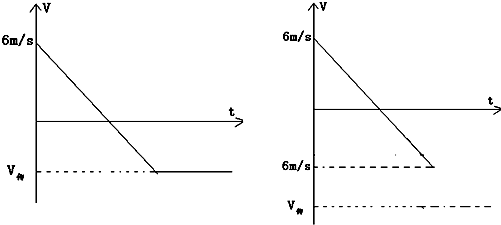
可知传送带速度越大两者的相对位移越小.综合以上分析传送带的速度为4m/s时,在传送带上放热最少.而在斜面上运动时,摩擦放热为定值.综上所述:
在斜面上摩擦放热:Q
1=μ
1mgcos37°
?=9J
物体在传送带上运动:Q
2=μ
2mg△x=50J
则摩擦总共放热:Q=Q
1+Q
2=59J
(4)若物体不脱离圆轨道形式有两种:一种是全部通过D点,一种是物块滑到CD的圆心高度以下.由图(3)的图象可知,由于传动速度足够大,则物体无论以什么样的速度滑上传送带,返回的速度均为原来的速度,物体的机械能损失全部发生在斜面上.
一、物体十次全部能经过D点:
设某次物体从左端滑上斜面理速度为v
n,滑上又滑下后的速度为v
n+1.
由能量守恒得:
上升过程:
m=mgh+μmgcos37°
? 下滑过程:
m=mgh-μmgcos37°
?得:
=
即每次滑上滑下斜面后,动能变为原来的
,数列为等比数列.
第十次滑上D点时,从经过EC滑上圆轨道的速度至少为4m/s,第十次
v102=16,则
v12=16×24=256,即物体第一次冲上圆轨道的速度为16m/s.
此时由释放点到B点动能定理:mgH
1-μmgcos37°
?=
m得:H
1=19.2m
则释放的最小高度为19.2m
二物体最高到达CD圆心高度,则由动能定理:mgH
2-μmgcos37°
?-mgR=0
得:H
2=0.24m
讨论:下面讨论物体是否存在能够在一次经过D点,经过斜面滑上滑下后到达不了CD圆心高度.
由于通过最高点机械能至少为
mg2R+m()2,经过一次滑上滑下斜面后,物体上圆轨道时机械能变为原来一半,则
(mg2R+m()2)>mgR.故不可能出现经过D点后下一次冲不到圆心高度的情况.
综上所述:H∈(0,0.24m]∪[19.2m,+∞)
答:(1)①第一次经过B点时的速度大小是6m/s.②第一次经过D点时轨道对物块的压力大小为62.5N.
(2)第二次通过最高点D点时轨道对物块的压力大小是28.125N.
(3)物块和各接触面摩擦至少要产生59J热量才能保证物体能够两次到达D点.
(4)释放物块的高度的要求为:H∈(0,0.24m]∪[19.2m,+∞).




 阅读快车系列答案
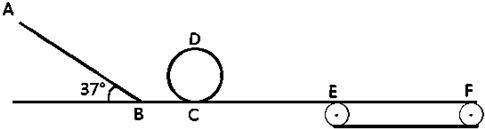
阅读快车系列答案 图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点推回到A点,设滑块与轨道间的动摩擦系数为μ,则推力对滑块做的功等于( )
图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD段是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计.一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓缓地由D点推回到A点,设滑块与轨道间的动摩擦系数为μ,则推力对滑块做的功等于( ) 如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且2AB=BC.小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,那么θ、μ1、μ2间应满足的关系是( )
如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且2AB=BC.小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,那么θ、μ1、μ2间应满足的关系是( )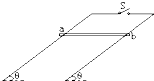 如图甲所示,在倾角为θ的斜面上固定有两根足够长的平行光滑导轨,轨距为L,金属导体棒ab垂直于两根轨道放在导轨上,导体ab的质量为m,电阻为R,导轨电阻不计,空间有垂直于导轨平面的匀强磁场,磁感应强度为B.当金属导体ab由静止开始向下滑动一段时间t0,再接通开关S,则关于导体ab运动的v-t图象可能正确的是( )
如图甲所示,在倾角为θ的斜面上固定有两根足够长的平行光滑导轨,轨距为L,金属导体棒ab垂直于两根轨道放在导轨上,导体ab的质量为m,电阻为R,导轨电阻不计,空间有垂直于导轨平面的匀强磁场,磁感应强度为B.当金属导体ab由静止开始向下滑动一段时间t0,再接通开关S,则关于导体ab运动的v-t图象可能正确的是( )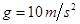 ,sin370=0.6,cos370=0.8。
,sin370=0.6,cos370=0.8。