
 如图,是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道,表演者骑着摩托车在竖直固定的圆轨道内做圆周运动,已知人和摩托车的总质量为m,轨道最高点B,轨道最低点A(重力加速度为g).求:
如图,是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道,表演者骑着摩托车在竖直固定的圆轨道内做圆周运动,已知人和摩托车的总质量为m,轨道最高点B,轨道最低点A(重力加速度为g).求:分析 (1)分析向心力来源,然后根据轨道只能提供支持力,不能提供拉力得到最小速度;
(2)分析向心力来源,由速度得到向心力,进而得到轨道对摩托车的支持力;
(3)分析向心力来源,由速度得到向心力,进而得到轨道对摩托车的支持力.
解答 解:(1)人和摩托车过最高点时,向心力的方向为竖直向下.在竖直方向上,人和摩托车受重力(G=mg,竖直向下)和轨道对摩托车的支持力(FN≥0,竖直向下)作用,
重力和支持力作为向心力,所以,有$G+{F}_{N}={F}_{向}=m\frac{{v}^{2}}{R}$,
因为FN≥0,所以,$G=mg=m\frac{{{v}_{min}}^{2}}{R}$,
所以,${v}_{min}=\sqrt{gR}$;
(2)由(1)可知,$G+{F}_{NB}={F}_{向}=m\frac{{v}^{2}}{R}$=$m\frac{2gR}{R}=2mg$,所以,FNB=mg;
(3)人和摩托车过A点时,向心力的方向为竖直向上.在竖直方向上,人和摩托车受重力(G=mg,竖直向下)和轨道对摩托车的支持力(FN≥0,竖直向上)作用,
重力和支持力作为向心力,所以,有${F}_{NA}-G={F}_{向}=m\frac{{v}^{2}}{R}$=$m\frac{6gR}{R}=6mg$,所以,FNA=7mg.
答:(1)人和摩托车能过最高点的最小速度${v}_{min}=\sqrt{gR}$;
(2)若人以v1=$\sqrt{2gR}$过B点轨道与摩托车之间的弹力FNB=mg;
(3)若人以v2=$\sqrt{6gR}$过A点轨道与摩托车之间的弹力FNA=7mg.
点评 物体能做圆周运动的临界条件就是轨道对物体的支持力刚好为零.对圆周运动的受力分析时,由于各位置向心力的方向不同,因此,要分别针对每个问题进行分析讨论.


科目:高中物理 来源: 题型:选择题
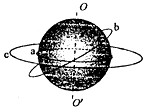 如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )
如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )| A. | a、b、c的向心加速度大小关系为ab>ac>aa | |
| B. | a、b、c的角速度大小关系为ωa>ωb>ωc | |
| C. | a、b、c的线速度大小关系为Va=Vb>Vc | |
| D. | a、b、c的周期关系为Ta>Tc>Tb |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 过山车在圆轨道上做匀速圆周运动 | |
| B. | 过山车在圆轨道最高点时的速度应为$\sqrt{gR}$ | |
| C. | 过山车在圆轨道最低点时乘客处于超重状态 | |
| D. | 过山车在圆轨道最高点时,轨道对它的支持力不能超过它的重力 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图甲所示,一质量为m=10kg的活塞在气缸内封闭一定质量的理想气体,开始时活塞距气缸底高度h1=1.00m.给气缸加热,活塞缓慢上升到距离气缸底h2=1.60m处,在此过程中缸内气体吸收了Q=700J的热量.已知活塞横截面积S=5.0×10-3m2,大气压强p0=1.0×105Pa,活塞与气缸壁间摩擦忽略不计,重力加速度g=10m/s2.求:
如图甲所示,一质量为m=10kg的活塞在气缸内封闭一定质量的理想气体,开始时活塞距气缸底高度h1=1.00m.给气缸加热,活塞缓慢上升到距离气缸底h2=1.60m处,在此过程中缸内气体吸收了Q=700J的热量.已知活塞横截面积S=5.0×10-3m2,大气压强p0=1.0×105Pa,活塞与气缸壁间摩擦忽略不计,重力加速度g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,细绳一端系着质量为M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔O吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,已知M和水平面的最大静摩擦力为2N.现使此平面绕中心轴转动,m处于静止状态,则角速度ω可能值为(取g=10m/s2)( )
如图所示,细绳一端系着质量为M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔O吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,已知M和水平面的最大静摩擦力为2N.现使此平面绕中心轴转动,m处于静止状态,则角速度ω可能值为(取g=10m/s2)( )| A. | 1rad/s | B. | 3rad/s | C. | 5rad/s | D. | 7rad/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 竖直分速度等于水平分速度 | B. | 即时速度的大小为 2v0 | ||
| C. | 运动时间为$\frac{{2v}_{0}}{g}$ | D. | 运动竖直方向位移为$\frac{{2\sqrt{2}{v}_{0}}^{2}}{g}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 气象研究小组用图示简易装置测定水平风速.在水平地面上竖直固定一直杆,半径为R、质量为m 的薄空心塑料球用细线悬于杆顶端O,当水平风吹来时,球在风力的作用下飘起来.已知风力大小正比于风速和球正对风的截面积,当风速v0=4m/s时,测得球平衡时细线与竖直方向的夹角θ=30°.则( )
气象研究小组用图示简易装置测定水平风速.在水平地面上竖直固定一直杆,半径为R、质量为m 的薄空心塑料球用细线悬于杆顶端O,当水平风吹来时,球在风力的作用下飘起来.已知风力大小正比于风速和球正对风的截面积,当风速v0=4m/s时,测得球平衡时细线与竖直方向的夹角θ=30°.则( )| A. | θ=60°时,风速v=6m/s | |
| B. | 若风速增大到某一值时,θ可能等于90° | |
| C. | 若风速不变,换用半径变大、质量不变的球,则θ不变 | |
| D. | 若风速不变,换用半径相等、质量变小的球,则θ增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 有一小铜块静止放置在倾角为α的方桌的桌布上,且位于方桌的中心.方桌布的一边与方桌的AB边重合,如图所示.已知小铜块与方桌布间的动摩擦因数为μ1,小铜块与方桌面间的动摩擦因数为μ2 (μ1>μ2>tan α).现突然以恒定的加速度a将桌布沿桌面向上抽离,加速度的方向是沿桌面的且垂直于AB边向上.若小铜块最后恰好未从方桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
有一小铜块静止放置在倾角为α的方桌的桌布上,且位于方桌的中心.方桌布的一边与方桌的AB边重合,如图所示.已知小铜块与方桌布间的动摩擦因数为μ1,小铜块与方桌面间的动摩擦因数为μ2 (μ1>μ2>tan α).现突然以恒定的加速度a将桌布沿桌面向上抽离,加速度的方向是沿桌面的且垂直于AB边向上.若小铜块最后恰好未从方桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com