
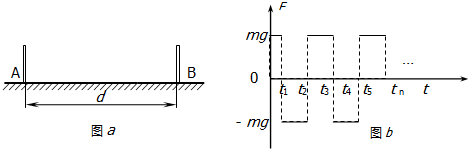
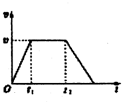
���� ��1���ʵ��B����A�����������˶������������˶���λ��֮�͵���$\frac{1}{2}$d�����ٶȹ�ʽ��λ�ƹ�ʽ��ʽ���t�ı���ʽ��
��2��Ѱ��ÿ�μ��ٺͼ��ٵĹ��ɣ��ó�tn�ı���ʽ��
��� �⣺��1���ʵ��˶����ٶȴ�Сa=$\frac{F}{m}$=g
��t=0ʱ��P��A��B����е�����������Ϊ0���ȼ����˶������ٶ�Ϊg������ʱ��t1��P���ٶȱ�Ϊv1����ʱ���ٶȱ�Ϊ����P�������ȼ����˶����پ���t1��P���ôﵽB�����ٶȱ�Ϊ0������
v1=g t1
0=v1-gt1
$\frac{1}{2}$d=$\frac{1}{2}$gt${\;}_{1}^{2}$+v1t1-$\frac{1}{2}$gt${\;}_{1}^{2}$
�����ϸ�ʽ��t1=t1=$\frac{\sqrt{2}}{2}$$\sqrt{\frac{d}{g}}$
��t=t1+t1=$\sqrt{2}$$\sqrt{\frac{d}{g}}$
��2��P��B�崦�������ȼ����˶�������ʱ��t2��P���ٶȱ�Ϊv2����������ʱ���ٶȱ�Ϊ���ң�P�������ȼ����˶����پ���t3��P���ôﵽA�����ٶȱ�Ϊ0������
v2=gt2
0=v2-gt3
d=$\frac{1}{2}$gt${\;}_{2}^{2}$+v2t3-$\frac{1}{2}$gt${\;}_{3}^{2}$
�����ϸ�ʽ�� t2=t3=$\sqrt{\frac{d}{g}}$
�� t2=t1+t1+t2=��$\sqrt{2}$+1��$\sqrt{\frac{d}{g}}$
�ʵ�P����A���������ȼ����˶�������ʱ��t4���ٶȱ�Ϊv3����ʱ���ٶȱ�Ϊ����P�������ȼ����˶�������t5��P���ôﵽB�����ٶȱ�Ϊ0������
v3=gt4
0=v3-gt5
d=$\frac{1}{2}$gt${\;}_{4}^{2}$+v3t5-$\frac{1}{2}$gt${\;}_{5}^{2}$
���ϵ� t4=t5=$\sqrt{\frac{d}{g}}$
t3=t2+t3+t4=��$\sqrt{2}$+3��$\sqrt{\frac{d}{g}}$
�����������������һ��P���е��˶������ҵ��⣬�Ժ�ÿ�δӴ�����ߵ����ұ�����ұߵ�����ߵ��˶������������ȼ����˶��������ȼ����˶�����ÿ���ȼ����˶����ȼ����˶���ʱ����ȣ���
t2=t3=t4=t5=��=$\sqrt{\frac{d}{g}}$
��tn=t+��2n-3��t2 ��n��2��
��tn=��$\sqrt{2}$+2n-3$\sqrt{\frac{d}{g}}$ ��n��2��
�𣺣�1���ʵ�P��AB���е�Ӿ�ֹ��ʼ������һ���˶������ҵ��ʱ��tΪ$\sqrt{2}\sqrt{\frac{d}{g}}$��
��2��ͼb��ʱ��${t}_{2}^{\;}��{t}_{3}^{\;}��{t}_{n}^{\;}$�ı���ʽ${t}_{2}^{\;}=\sqrt{\frac{d}{g}}$��${t}_{3}^{\;}=��\sqrt{2}+3��\sqrt{\frac{d}{g}}$��${t}_{n}^{\;}=��\sqrt{2}+2n-3��\sqrt{\frac{d}{g}}$��
���� �������ʵ��������Ա仯�������������µ��˶����⣬�����ʵ���˶�����������˶������ǹؼ���


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �������ʧȥ��������Լ���ͻ�ɢ����������Ϊ�������֮����ڳ�����Ե�� | |
| B�� | �����Ӽ�������ͳ���ƽ��ʱ������������С | |
| C�� | һ����100���ˮ���100���ˮ�����������֮����������� | |
| D�� | һ���������壬��ѹǿ����ʱ������ÿ������ڵ�λ���ƽ����ײ���������¶Ƚ��Ͷ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
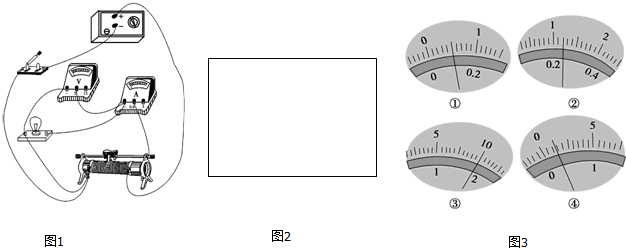
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������ƻ�����֮��ľ��벻��� | |
| B�� | �ú����ʵ������Ϲ���ʵ��õ������������ƣ������ƣ�֮��ļ���� | |
| C�� | ����ij�㵽˫��ľ���֮����ڰ��������������ʱ����㽫���ְ����� | |
| D�� | ������ð���ʵ�飬��������֮��ľ�������ȵ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
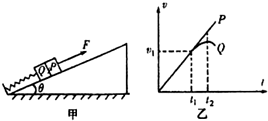 ��ͼ����ʾ��ƽ����б����ᵯ�ɣ�����ϵ��Ϊk��һ�˹̶������Ϊ�ȵ�б��ˣ���һ����Q������ӣ�P��Q������Ϊm��б��⻬�ҹ̶���ˮƽ���ϣ���ʼʱ������ֹ������ƽ����б�����ϵ���F�����P��ʹP�����ٶ�Ϊa���ȼ����˶�����������ڿ�ʼһ��ʱ���ڵ�v-tͼ����ͼ����ʾ���������ٶ�Ϊg����������
��ͼ����ʾ��ƽ����б����ᵯ�ɣ�����ϵ��Ϊk��һ�˹̶������Ϊ�ȵ�б��ˣ���һ����Q������ӣ�P��Q������Ϊm��б��⻬�ҹ̶���ˮƽ���ϣ���ʼʱ������ֹ������ƽ����б�����ϵ���F�����P��ʹP�����ٶ�Ϊa���ȼ����˶�����������ڿ�ʼһ��ʱ���ڵ�v-tͼ����ͼ����ʾ���������ٶ�Ϊg����������| A�� | ʩ������ǰ��Q��P������СΪmgsin�� | |
| B�� | ʩ������ǰ�����ɵ��α���Ϊ$\frac{2mgsin��}{k}$ | |
| C�� | ��t1ʱ�̣������ͷŵĵ�������Ϊ$\frac{1}{2}$mv12 | |
| D�� | t2ʱ�̵��ɻָ���ԭ�������Q�ﵽ�ٶ����ֵ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
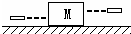 ����ΪM�ľ���ľ�龲ֹ�ڹ⻬ˮƽ���ϣ�ľ�������������һλ������ȫ��ͬ��ǹ���ӵ�������֣�����������ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd1��Ȼ���Ҳ����ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd2����ͼ���ӵ���δ�䴩ľ�飬�ӵ�����Ϊm��M=2m���������ӵ���ľ��֮�����������С����ͬ�����������ӵ������ľ�龲ֹʱd1�� d2�ı�ֵ��
����ΪM�ľ���ľ�龲ֹ�ڹ⻬ˮƽ���ϣ�ľ�������������һλ������ȫ��ͬ��ǹ���ӵ�������֣�����������ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd1��Ȼ���Ҳ����ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd2����ͼ���ӵ���δ�䴩ľ�飬�ӵ�����Ϊm��M=2m���������ӵ���ľ��֮�����������С����ͬ�����������ӵ������ľ�龲ֹʱd1�� d2�ı�ֵ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 һλͬѧ�ļ�ס��һ��25��ĸ�¥�ڣ���ÿ��˵�����¥��������ѧ����֪ʶ�����࣬��һ����ͻȻ�뵽���ܷ�����ѧ����֪ʶ��Ϊȷ�ز������¥�ĸ߶��أ����Ժ��һ��ʱ�����������˶��ʵ��������������£�
һλͬѧ�ļ�ס��һ��25��ĸ�¥�ڣ���ÿ��˵�����¥��������ѧ����֪ʶ�����࣬��һ����ͻȻ�뵽���ܷ�����ѧ����֪ʶ��Ϊȷ�ز������¥�ĸ߶��أ����Ժ��һ��ʱ�����������˶��ʵ��������������£�| ʱ��/s | ��������ǰ | 0��3.0 | 3.0��13.0 | 13.0��19.0 | 19.0�Ժ� |
| ̨��ʾ��/kg | 5.0 | 5.0 | 4.6 | 5.0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com