
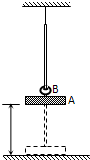
 如图所示,底座A上装有长0.5m的直立杆,总质量为1kg,用细线悬挂,底座底面离水平地面H=0.2m,杆上套有质量为0.2kg的小环B,它与杆间有摩擦,设环与杆相对滑动时摩擦力大小始终不变,环从底座以
如图所示,底座A上装有长0.5m的直立杆,总质量为1kg,用细线悬挂,底座底面离水平地面H=0.2m,杆上套有质量为0.2kg的小环B,它与杆间有摩擦,设环与杆相对滑动时摩擦力大小始终不变,环从底座以 m/s的初速度沿杆向上运动,最后恰能到达杆的顶端(取g=10m/s2).求:
m/s的初速度沿杆向上运动,最后恰能到达杆的顶端(取g=10m/s2).求: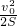 =15m/s2
=15m/s2  gt12
gt12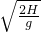 =0.2s
=0.2s  a2t22
a2t22 

科目:高中物理 来源: 题型:
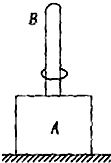 如图所示,底座A上装有长0.5m的直立杆,其总质量为0.2kg,杆上套有质量为0.05kg的小环B,它与杆有摩擦.当环从座上以4m/s的速度起飞时,刚好能到达杆顶,求:
如图所示,底座A上装有长0.5m的直立杆,其总质量为0.2kg,杆上套有质量为0.05kg的小环B,它与杆有摩擦.当环从座上以4m/s的速度起飞时,刚好能到达杆顶,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,底座A上装有长0.5m的直立杆,其总质量为0.2kg,杆上套有0.05kg的小环B,与杆有摩擦.当环以4m/s的初速度从底座向上运动,刚好能到达杆顶(A始终处于静止状态)求:
如图所示,底座A上装有长0.5m的直立杆,其总质量为0.2kg,杆上套有0.05kg的小环B,与杆有摩擦.当环以4m/s的初速度从底座向上运动,刚好能到达杆顶(A始终处于静止状态)求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,底座A上装有长0.5m的直立杆,总质量为1kg,用细线悬挂,底座底面离水平地面H=0.2m,杆上套有质量为0.2kg的小环B,它与杆间有摩擦,设环与杆相对滑动时摩擦力大小始终不变,环从底座以
如图所示,底座A上装有长0.5m的直立杆,总质量为1kg,用细线悬挂,底座底面离水平地面H=0.2m,杆上套有质量为0.2kg的小环B,它与杆间有摩擦,设环与杆相对滑动时摩擦力大小始终不变,环从底座以| 15 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,底座A上装有长s=0.5m的直立杆,质量M=0.2kg,杆上套有m=0.05kg的小环B,它与杆之间有摩擦.若环从底座上以v0=4m/s的速度飞起,刚好能到达杆顶(g=10m/s2).下列说法错误的是( )
如图所示,底座A上装有长s=0.5m的直立杆,质量M=0.2kg,杆上套有m=0.05kg的小环B,它与杆之间有摩擦.若环从底座上以v0=4m/s的速度飞起,刚好能到达杆顶(g=10m/s2).下列说法错误的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,底座A上装有长0.5m的直立杆,总质量为0.2kg,杆上套有质量为0.05kg的小环B,它与杆之间接有摩擦.若环从底座上以4m/s的速度飞起,则刚好能到达杆顶.求:
如图所示,底座A上装有长0.5m的直立杆,总质量为0.2kg,杆上套有质量为0.05kg的小环B,它与杆之间接有摩擦.若环从底座上以4m/s的速度飞起,则刚好能到达杆顶.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com