
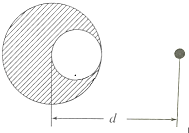
 如图所示,在半径为R的铅球中挖出一个球星空穴,空穴与球相切,并通过铅球的球心,在未挖去空穴前铅球质量为M,求有空穴的铅球对与铅球球心距离为d的质量为m的小球的万有引力是多大?
如图所示,在半径为R的铅球中挖出一个球星空穴,空穴与球相切,并通过铅球的球心,在未挖去空穴前铅球质量为M,求有空穴的铅球对与铅球球心距离为d的质量为m的小球的万有引力是多大? 分析 用没挖之前球对质点的引力,减去被挖部分对质点的引力,就是剩余部分对质点的引力.
解答 解:
球体密度为:ρ=$\frac{M}{\frac{4π{R}^{3}}{3}}$.
则m=$ρ•\frac{4π(\frac{R}{2})^{3}}{3}$=$\frac{M}{8}$
由万有引力表达式挖去前的引力为:F=G$\frac{Mm}{{r}^{2}}$=$\frac{GMm}{{d}^{2}}$,
被挖部分对质点的引力为:F′=$\frac{G\frac{M}{8}m}{(d-\frac{R}{2})^{2}}$,剩余部分的引力为:F-F′=$GMm(\frac{1}{{d}^{2}}-\frac{1}{8(d-0.5R)^{2}})$
答:剩余部分对m2的万有引力为$GMm(\frac{1}{{d}^{2}}-\frac{1}{8(d-0.5R)^{2}})$
点评 本题的关键就是要对挖之前的引力和挖去部分的引力计算,而不是直接去计算剩余部分的引力,因为那是一个不规则球体,其引力直接由公式得到.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中物理 来源: 题型:解答题
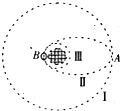 按照我国整个月球探测活动的计划,在第一步“绕月”工程圆满完成各项目标和科 学探测任务后,将开展第二步“落月”工程.如图所示 假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ上运动,当运动到轨道 上的A点时,点火变轨进人椭圆轨道Ⅱ,在到达轨道的近 月点B时再次点火变轨,进入近月轨道DI绕月球做圆周运动.求:
按照我国整个月球探测活动的计划,在第一步“绕月”工程圆满完成各项目标和科 学探测任务后,将开展第二步“落月”工程.如图所示 假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ上运动,当运动到轨道 上的A点时,点火变轨进人椭圆轨道Ⅱ,在到达轨道的近 月点B时再次点火变轨,进入近月轨道DI绕月球做圆周运动.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
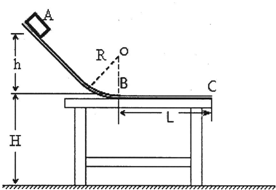 如图所示,滑块从A点沿光滑轨道滑出B点,并进入动摩擦因数为μ=0.5的水平粗糙轨道,倾斜部分与水平部分之间是由一段半径为R的圆弧轨道光滑连接,图中h=L=2R,
如图所示,滑块从A点沿光滑轨道滑出B点,并进入动摩擦因数为μ=0.5的水平粗糙轨道,倾斜部分与水平部分之间是由一段半径为R的圆弧轨道光滑连接,图中h=L=2R,查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一光滑圆锥体固定在水平面上,OC⊥AB,∠AOC=30°,一条不计质量、长为L的绳(L<OA)一端固定在顶点O,另一端拴一质量为m的物体(看作质点).物体以速度v绕圆锥体的轴线OC在水平面内作匀速圆周运动.
如图所示,一光滑圆锥体固定在水平面上,OC⊥AB,∠AOC=30°,一条不计质量、长为L的绳(L<OA)一端固定在顶点O,另一端拴一质量为m的物体(看作质点).物体以速度v绕圆锥体的轴线OC在水平面内作匀速圆周运动.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | vf | B. | $\frac{v}{f}$ | C. | $\frac{f}{v}$ | D. | f |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
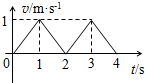
| A. | 做匀速直线运动 | B. | 做匀加速直线运动 | ||
| C. | 一直朝某一方向运动 | D. | 在某一线段上做两个来回运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com