
 在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )
在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )| A. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B. | $\frac{2π}{{ω}_{0}+\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C. | $\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | D. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0}}$ |
分析 在地球表面重力与万有引力大小相等,根据卫星的轨道半径求得卫星的角速度,所以卫星再次经过这个位置需要最短时间为卫星转动比地球转动多一周,从而求得最短时间.
解答 解:在地球表面重力与万有引力相等有:
$G\frac{mM}{{R}^{2}}=mg$
所以有:GM=gR2
所以卫星的轨道半径r,万有引力提供圆周运动向心力有:
$G\frac{mM}{{r}^{2}}=mr{ω}^{2}$
可得该卫星的角速度$ω=\sqrt{\frac{GM}{{r}^{3}}}$=$\sqrt{\frac{g{R}^{2}}{{r}^{3}}}$
所以当卫星再次经过该建筑物上空时,卫星比地球多转动一周,所用时间:
t=$\frac{2π}{|ω-{ω}_{0}|}$
故时间可能为:$\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0}}$或$\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$
故AB错误,BD正确.
故选:BD.
点评 能根据地面重力与万有引力相等和万有引力提供圆周运动向心力由卫星轨道半径求得卫星的角速度,根据运动关系求时间这是正确解题问题的关键.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中物理 来源: 题型:解答题
 如图所示,在某一水平面上有一轨道AC,其中AB段光滑,BC段粗糙,BC段与滑块之间的动摩擦因数为μ=0.2,有一质量为m=2kg的滑块从A点出发,以初速度v0=4m/s向右运动,恰能到达BC的中点,若滑块以初速度v0=4m/s从A点滑出的同时,给物体施加一水平向右、大小为1N的力F,则物体刚好能到达C,求:
如图所示,在某一水平面上有一轨道AC,其中AB段光滑,BC段粗糙,BC段与滑块之间的动摩擦因数为μ=0.2,有一质量为m=2kg的滑块从A点出发,以初速度v0=4m/s向右运动,恰能到达BC的中点,若滑块以初速度v0=4m/s从A点滑出的同时,给物体施加一水平向右、大小为1N的力F,则物体刚好能到达C,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
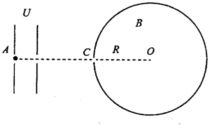 在光滑绝缘的水平面上,左侧平行极板间有水平方向匀强电场,右侧圆筒内有竖直方向匀强磁场,磁感应强度大小为B,俯视图如图所示,圆的圆心为O点,半径大小为R,一质量为m、电荷量大小为q的带电小球(可视为质点),初速位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,粒子和圆筒壁的碰撞没有动能和电荷量损失,B、R、m、q为已知量,圆筒仅有一个出入口C.
在光滑绝缘的水平面上,左侧平行极板间有水平方向匀强电场,右侧圆筒内有竖直方向匀强磁场,磁感应强度大小为B,俯视图如图所示,圆的圆心为O点,半径大小为R,一质量为m、电荷量大小为q的带电小球(可视为质点),初速位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,粒子和圆筒壁的碰撞没有动能和电荷量损失,B、R、m、q为已知量,圆筒仅有一个出入口C.查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,真空中存在空间范围足够大、方向水平向右的匀强磁场,在电场中,一个质量为m、电荷量为q的离子,以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动.
如图所示,真空中存在空间范围足够大、方向水平向右的匀强磁场,在电场中,一个质量为m、电荷量为q的离子,以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动.查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
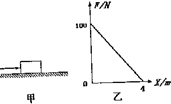 如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )
如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )| A. | 物体先做加速运动,推力撤去时开始做减速运动 | |
| B. | 物体在水平面上运动的最大位移是10m | |
| C. | 物体运动的最大速度为2$\sqrt{15}$m/s | |
| D. | 物体在运动中的加速度先变小后不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com