

分析 (1)抓住挑战者在A点刚好对管壁无压力,可以求出小球经过A点时的速度大小,再从静止开始下滑到经过A点的过程中只有重力对挑战者做功,根据动能定理求得挑战者下滑的高度h;
(2)同理抓住在B点对管壁压力大小可以求得经过B点时的速度大小,然后从A到B的过程中有重力做功和CD段的阻力做功,根据动能定理求得阻力做功;
(3)挑战者滑离平台后做平抛运动,根据运动的合成与分解可以求得入水时的速度大小.
解答 解:(1)挑战者在A点对管壁无压力,则挑战者仅受重力作用,根据牛顿第二定律有:mg=m$\frac{{v}_{A}^{2}}{R}$
可得挑战者在A点的速度为:vA=$\sqrt{gR}$
设挑战者从离水平轨道高为H处开始下滑,从静止开始到A点只有重力做功,根据动能定理有:mg(H-2R)=$\frac{1}{2}$mv${\;}_{A}^{2}$-0
可得:H=$\frac{\frac{1}{2}m{v}_{A}^{2}+2mgR}{mg}$=$\frac{\frac{1}{2}mgR+2mgR}{mg}$=$\frac{5}{2}$R
(2)因为挑战者在B点对管的内侧壁压力为0.5mg,故满足:mg+NB=m$\frac{{v}_{B}^{2}}{r}$
可得:vB=$\sqrt{1.5gr}$
又因为挑战者从A滑至B点过程中只有重力做功和阻力在CD段做功,
根据动能定理有:mg(2R-2r)-Wf克=$\frac{1}{2}$mv${\;}_{B}^{2}$$-\frac{1}{2}m{v}_{A}^{2}$
所以有:Wf克=mg(2R-2r)+$\frac{1}{2}$m${v}_{A}^{2}$-$\frac{1}{2}$mv${\;}_{B}^{2}$=2.25mgr-$\frac{11}{4}$mgR;
(3)挑战者从B到落水的过程中只有重力做功,根据动能定理有:mg•2r+mgh=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}$mv${\;}_{B}^{2}$
可得:v=$\sqrt{2×2gr+2×2.25gr+1.5gr}$=$\sqrt{11gr}$
答:(1)挑战者若能完成上述过程,则他应从离水平轨道$\frac{5}{2}$R高的地方开始下滑;
(2)挑战者从A到B的运动过程中克服轨道阻力所做的功为2.25mgr-$\frac{11}{4}$mgR;
(3)挑战者入水时速度的大小为$\sqrt{11gr}$.
点评 本题是多过程问题,应用动能定理时要灵活选择研究的过程,正确的进行受力分析和做功分析是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题
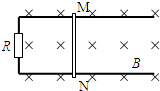 如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计.
如图所示,宽度为L的足够长的平行金属导轨固定在绝缘水平面上,导轨的两端连接阻值R的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B,一根质量m的导体棒MN放在导轨上与导轨接触良好,导体棒的有效电阻也为R,导体棒与导轨间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.导体棒MN的初始位置与导轨最左端距离为L,导轨的电阻可忽略不计.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 长为1.0m的长木板B静止放在水平冰面上,小物块A以某一初速度从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为0.4m/s,然后A、B又一起在水平冰面上滑行了16.0cm后停下.若小物块A可视为质点,它与长木板B的质量相同都为2kg,A、B间的动摩擦因数μ1=0.20.求:(取g=10m/s2)
长为1.0m的长木板B静止放在水平冰面上,小物块A以某一初速度从木板B的左端滑上长木板B,直到A、B的速度达到相同,此时A、B的速度为0.4m/s,然后A、B又一起在水平冰面上滑行了16.0cm后停下.若小物块A可视为质点,它与长木板B的质量相同都为2kg,A、B间的动摩擦因数μ1=0.20.求:(取g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平地面上竖直固定一个光滑的,半径R=0.45m的$\frac{1}{4}$圆弧轨道,A、B分别是圆弧的端点,圆弧B点右侧是光滑的水平地面,地面上放着一块足够长的木板,木板的上表面与圆弧轨道的最低点B等高,可视为质点的小滑块P1和P2的质量均为m=0.2kg,木板的质量M=4m,P1和P2与木板上表面的动摩擦因数分别为μ1=0.20和μ2=0.50,最大静摩擦力近似等于滑动摩擦力,开始时木板的左端紧靠着B,P2静止在木板的左端,P1以v0=4.0m/s的初速度从A点沿圆弧轨道自由滑下,与P2发生弹性碰撞后,P1处在木板的左端,取g=10m/s2.求:
如图所示,水平地面上竖直固定一个光滑的,半径R=0.45m的$\frac{1}{4}$圆弧轨道,A、B分别是圆弧的端点,圆弧B点右侧是光滑的水平地面,地面上放着一块足够长的木板,木板的上表面与圆弧轨道的最低点B等高,可视为质点的小滑块P1和P2的质量均为m=0.2kg,木板的质量M=4m,P1和P2与木板上表面的动摩擦因数分别为μ1=0.20和μ2=0.50,最大静摩擦力近似等于滑动摩擦力,开始时木板的左端紧靠着B,P2静止在木板的左端,P1以v0=4.0m/s的初速度从A点沿圆弧轨道自由滑下,与P2发生弹性碰撞后,P1处在木板的左端,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )
在印度尼西亚的坤甸有一座著名的建筑,它正好建在赤道上,若某人造地球卫星在赤道上空飞行,卫星的轨道平面与地球赤道重合,已知卫星轨道半径为r,飞行方向与地球的自转方向相同,地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,卫星在某时刻通过这一建筑物的正上方,则该卫星再次经过这个位置需要的最短时间为( )| A. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | B. | $\frac{2π}{{ω}_{0}+\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | C. | $\frac{2π}{{ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}}}$ | D. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 作简谐运动的物体每次通过同一位置时都具有相同的加速度和速度 | |
| B. | 横波在传播过程中,波峰上的质点运动到相邻的波峰所用的时间为一个周期 | |
| C. | 一束光由介质斜射向空气,界面上可能只发生反射现象而没有折射现象 | |
| D. | 水面油膜呈现彩色条纹是光的干涉现象,这说明了光是一种波 | |
| E. | 在电场周围一定存在磁场,在磁场周围一定存在电场 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com