
 如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计带电粒子的重力.
如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计带电粒子的重力.| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| qEt2 |
| 2m |
| qEL2 | ||
2m
|
| 4Ek |
| qL |
| 1 |
| 2 |
2
| ||
| qL |
| Ek′-Ek |
| qL |
2
| ||
| qL |
| Ek′-Ek |
| qL |


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中物理 来源: 题型:
 如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )
如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
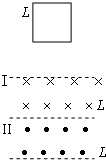 如图所示,边长为L的正方形导线框底边水平,且平行于正下方的磁场边界,正下方的匀强磁场宽度均为L,磁感强度等值反向,两磁场区域紧邻.当线框底边进入磁场I区域时,导线框恰好做匀速运动,这时导线框的电功率为P.则当导线框底边刚进入磁场II区域时,下列结论正确的是( )
如图所示,边长为L的正方形导线框底边水平,且平行于正下方的磁场边界,正下方的匀强磁场宽度均为L,磁感强度等值反向,两磁场区域紧邻.当线框底边进入磁场I区域时,导线框恰好做匀速运动,这时导线框的电功率为P.则当导线框底边刚进入磁场II区域时,下列结论正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
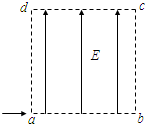 如图所示,边长为L的正方形区域abcd内存在着匀强电场,一个质量为m、电量为q、初速度为v0的带电
如图所示,边长为L的正方形区域abcd内存在着匀强电场,一个质量为m、电量为q、初速度为v0的带电查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,边长为L的正方形闭合线框,在磁感应强度为B的匀强磁场中,以一条边为轴,以角速度ω匀速转动,转轴与B垂直,线圈总电阻为R,导线电阻不计.下列说法中正确的是( )
如图所示,边长为L的正方形闭合线框,在磁感应强度为B的匀强磁场中,以一条边为轴,以角速度ω匀速转动,转轴与B垂直,线圈总电阻为R,导线电阻不计.下列说法中正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com