
 如图所示,质量mA=0.8kg、带电量q=-4×10-3C的A球用长度l=0.8m的不可伸长的绝缘轻线悬吊在O点,O点右侧有竖直向下的匀强电场,场强E=5×103N/C.质量mB=0.2kg不带电的B球静止在光滑水平轨道上,右侧紧贴着压缩并锁定的轻质弹簧,弹簧右端与固定挡板连接,弹性势能为3.6J.现将A球拉至左边与圆心等高处释放,将弹簧解除锁定,B球离开弹簧后,恰好与第一次运动到最低点的A球相碰,并结合为一整体C,同时撤去水平轨道.A、B、C均可视为质点,线始终未被拉断,g=10m/s2.求:
如图所示,质量mA=0.8kg、带电量q=-4×10-3C的A球用长度l=0.8m的不可伸长的绝缘轻线悬吊在O点,O点右侧有竖直向下的匀强电场,场强E=5×103N/C.质量mB=0.2kg不带电的B球静止在光滑水平轨道上,右侧紧贴着压缩并锁定的轻质弹簧,弹簧右端与固定挡板连接,弹性势能为3.6J.现将A球拉至左边与圆心等高处释放,将弹簧解除锁定,B球离开弹簧后,恰好与第一次运动到最低点的A球相碰,并结合为一整体C,同时撤去水平轨道.A、B、C均可视为质点,线始终未被拉断,g=10m/s2.求:分析 (1)根据机械能守恒求出A球摆到最低点的速度,由B球弹性势能转化为小球的动能求出B球碰前速度,根据系统动量守恒定律求出碰后整体的速度C,由动能定理即可求解碰撞过程A球对B球所做的功;
(2)碰后整体做类平抛运动,根据类平抛运动的规律求出绳子刚好拉直时的速度,再由动能定理求出碰后C第一次离开电场时的速度;
(3)根据动能定理和向心力的知识列式即可求解;
解答 解:(1)碰前A的速度
$\frac{1}{2}{m}_{A}^{\;}{v}_{A}^{2}={m}_{A}^{\;}gl$
解得:${v}_{A}^{\;}=\sqrt{2gl}=\sqrt{2×10×0.8}m/s=4m/s$
碰前B的速度$E=\frac{1}{2}{m}_{B}^{\;}{v}_{B}^{2}$
解得:${v}_{B}^{\;}=\sqrt{\frac{2E}{{m}_{B}^{\;}}}=\sqrt{\frac{2×3.6}{0.2}}=6m/s$
由由动量守恒得:
${m}_{A}^{\;}{v}_{A}^{\;}-{m}_{B}^{\;}{v}_{B}^{\;}=({m}_{A}^{\;}+{m}_{B}^{\;}){v}_{AB}^{\;}$
代入数据:
$0.8×4-0.2×6=(0.8+0.2){v}_{AB}^{\;}$
解得:${v}_{AB}^{\;}=2m/s$
A对B所做的功$W=\frac{1}{2}{m}_{B}^{\;}{v}_{AB}^{2}-\frac{1}{2}{m}_{B}^{\;}{v}_{B}^{2}$=$\frac{1}{2}×0.2×{2}_{\;}^{2}-\frac{1}{2}×0.2×{6}_{\;}^{2}=-3.2J$
(2)碰后,整体受到电场力$F=qE=4×1{0}_{\;}^{-3}×5×1{0}_{\;}^{3}=20N$
$G={m}_{C}^{\;}g=(0.8+0.2)×10=10N$
因$F-{m}_{C}^{\;}g>{m}_{C}^{\;}\frac{{v}_{\;}^{2}}{l}$,
小球做类平抛运动
水平方向上:
$x={v}_{C}^{\;}t$
竖直方向上:
$y=\frac{1}{2}a{t}_{\;}^{2}$
其中$a=\frac{qE-{m}_{C}^{\;}g}{{m}_{C}^{\;}}$=$\frac{20-10}{0.8+0.2}=10m/{s}_{\;}^{2}$
圆的方程:
$(y-l)_{\;}^{2}+{x}_{\;}^{2}={l}_{\;}^{2}$
解得:x=0..8m y=0.8m t=0.4s
C刚好在圆心等高处绳子拉直
设此时C向上的速度为${v}_{1}^{\;}=at=10×0.4=4m/s$
设小球运动到最高点速度为${v}_{2}^{\;}$
由动能定理得:
$\frac{1}{2}{m}_{C}^{\;}{v}_{2}^{2}-\frac{1}{2}{m}_{C}^{\;}{v}_{1}^{2}=(F-{m}_{C}^{\;}g)l$
代入数据:$\frac{1}{2}×1{v}_{2}^{2}-\frac{1}{2}×1×{4}_{\;}^{2}=(20-10)×0.8$
解得:${v}_{2}^{\;}=4\sqrt{2}$m/s=5.66m/s
(3)设小球从最高点运动到最低点时的速度为${v}_{3}^{\;}$得:
$\frac{1}{2}{m}_{C}^{\;}{v}_{3}^{2}-\frac{1}{2}{m}_{C}^{\;}{v}_{2}^{2}={m}_{C}^{\;}g×2l$
代入数据:$\frac{1}{2}×1{v}_{3}^{2}-\frac{1}{2}×1×(4\sqrt{2})_{\;}^{2}=1×10×2×0.8$
解得:${v}_{3}^{\;}=8m/s$
由$T+F-{m}_{C}^{\;}g={m}_{C}^{\;}\frac{{v}_{3}^{2}}{l}$
解得T=70N>0,所以小球能一直做圆周运动
设经过最高点次数为n
$\frac{1}{2}{m}_{C}^{\;}{v}_{n}^{2}-\frac{1}{2}{m}_{C}^{\;}{v}_{2}^{2}=(n-1)qE×2l$
$T+{m}_{C}^{\;}g-F≥{m}_{C}^{\;}\frac{{v}_{n}^{2}}{l}$
解得:$T=(80n-30)N\\;\\;\\;\$ n=1,2,3,…
答:(1)碰撞过程中A球对B球做的功为-3.2J
(2)碰后C第一次离开电场时的速度5.66m/s
(3)C每次离开电场前瞬间绳子受到的拉力为(80n-30)N(n=0、1、2…).
点评 本题主要考查了动能定理、动量守恒定律、牛顿第二定律及功能关系的应用,要求同学们能正确分析物体的受力情况及运动过程,难度较大.


科目:高中物理 来源: 题型:选择题
| A. | 洛伦兹力的大小与速度无关 | B. | 洛伦兹力不改变带电粒子的速度 | ||
| C. | 洛伦兹力对带电粒子做功 | D. | 洛伦兹力不改变带电粒子的动能 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 任意两段时间内速度变化的方向相同 | |
| B. | 任意两段时间内速度变化的大小相等 | |
| C. | 当竖直位移等于水平位移时,竖直方向的平均速度与水平方向的平均速度也相等 | |
| D. | 速度与水平方向夹角的正切值总等于位移与水平方向夹角的正切值的两倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
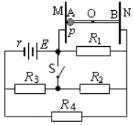 如图所示电路,电源电动势E=4.8V,内阻r=0.4Ω,电阻R1=R2=R3=4Ω,R4=2Ω,R1两端连接一对竖直放置的平行金属板M、N,板间电场视为匀强电场.板间固定一根与板面垂直,长度与板间距相等的光滑绝缘细杆AB,AB上套一个质量m=2.6×10-4kg的带电环P,P的电荷量为q=+2×10-4C(视为点电荷,不影响电场分布),电键S断开时,将带电环P从杆的左端A处由静止释放,P运动到杆的中点O时,开关S闭合,求:
如图所示电路,电源电动势E=4.8V,内阻r=0.4Ω,电阻R1=R2=R3=4Ω,R4=2Ω,R1两端连接一对竖直放置的平行金属板M、N,板间电场视为匀强电场.板间固定一根与板面垂直,长度与板间距相等的光滑绝缘细杆AB,AB上套一个质量m=2.6×10-4kg的带电环P,P的电荷量为q=+2×10-4C(视为点电荷,不影响电场分布),电键S断开时,将带电环P从杆的左端A处由静止释放,P运动到杆的中点O时,开关S闭合,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,质量分别为2m和m的A、B两球用细线悬挂于天花板上且静止不动.两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间,A、B两球的加速度大小分别为aA=15m/s2;aB=0m/s2.
如图所示,质量分别为2m和m的A、B两球用细线悬挂于天花板上且静止不动.两球间是一个轻质弹簧,如果突然剪断悬线,则在剪断悬线瞬间,A、B两球的加速度大小分别为aA=15m/s2;aB=0m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
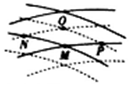 如图所示,两个波源在水面上传播并产生干涉现象,其中实线和虚线分别表示振幅均为A的两列波的波峰和波谷,t=0时刻M是波峰与波峰相遇的点,下列说法正确的是( )
如图所示,两个波源在水面上传播并产生干涉现象,其中实线和虚线分别表示振幅均为A的两列波的波峰和波谷,t=0时刻M是波峰与波峰相遇的点,下列说法正确的是( )| A. | 质点O、M的振动频率相等 | |
| B. | 质点P振动的振幅为A | |
| C. | 质点M振动的振幅为A | |
| D. | 质点M振动一个周期,其路程为8A | |
| E. | 若质点M振动的频率为2.5Hz,则从图示时刻起经1.7s后质点M的运动方向竖直向下 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 北京时间2016年10月19日凌晨3点,神舟十一号飞船与天宫二号空间实验室成功实现自动交会对接,如图所示,已知神舟十一号飞船从捕获天宫二号实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道高度不变,速度大小不变),地球半径为R,地球表面重力加速度为g,引力常量为G,忽略地球自转,则( )
北京时间2016年10月19日凌晨3点,神舟十一号飞船与天宫二号空间实验室成功实现自动交会对接,如图所示,已知神舟十一号飞船从捕获天宫二号实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道高度不变,速度大小不变),地球半径为R,地球表面重力加速度为g,引力常量为G,忽略地球自转,则( )| A. | 组合体运动的周期T=$\frac{2πt}{θ}$ | |
| B. | 组合体运动的速度大小v=$\root{3}{g{R}^{2}}$ | |
| C. | 组合体的向心加速度a=$\root{3}{\frac{g{R}^{2}{θ}^{4}}{{t}^{4}}}$ | |
| D. | 组合体所在圆轨道的半径r=$\root{3}{\frac{g{R}^{2}{t}^{2}}{{θ}^{2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com