
 如图所示,光滑水平面MN的左端M处有一弹射装置P,右端N处与水平传送带恰平齐接触,传送带水平部分长度L=16m,沿逆时针方向以恒定速度v=2m/s匀速转动.ABCDE是由三部分光滑轨道平滑连接在一起组成的,AB为水平轨道,弧BCD是半径为R的半圆弧轨道,弧DE是半径为2R的圆弧轨道,弧BCD与弧DE相切在轨道最高点D,R=0.6m.水平部分A点与传送带平齐接触.放在MN段的物块m(可视为质点)以初速度v0=4m/s冲上传送带,物块与传送带间的动摩擦因数μ=0.2,物块的质量m=1kg,结果物块滑上传送带运动一段时间后,又返回到N端,经水平面与左端M处的固定弹射器相碰撞(弹射器的弹簧原来被压缩后被锁定),因碰撞使弹射器的锁定被打开,将物块弹回后滑过传送带,冲上右侧的圆弧轨道,物块恰能始终贴着圆弧轨道BCDE内侧通过其最高点D后,从E点飞出.g=10m/s2.求:
如图所示,光滑水平面MN的左端M处有一弹射装置P,右端N处与水平传送带恰平齐接触,传送带水平部分长度L=16m,沿逆时针方向以恒定速度v=2m/s匀速转动.ABCDE是由三部分光滑轨道平滑连接在一起组成的,AB为水平轨道,弧BCD是半径为R的半圆弧轨道,弧DE是半径为2R的圆弧轨道,弧BCD与弧DE相切在轨道最高点D,R=0.6m.水平部分A点与传送带平齐接触.放在MN段的物块m(可视为质点)以初速度v0=4m/s冲上传送带,物块与传送带间的动摩擦因数μ=0.2,物块的质量m=1kg,结果物块滑上传送带运动一段时间后,又返回到N端,经水平面与左端M处的固定弹射器相碰撞(弹射器的弹簧原来被压缩后被锁定),因碰撞使弹射器的锁定被打开,将物块弹回后滑过传送带,冲上右侧的圆弧轨道,物块恰能始终贴着圆弧轨道BCDE内侧通过其最高点D后,从E点飞出.g=10m/s2.求: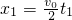 =4m;
=4m; =1s
=1s
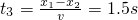 ;
;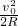
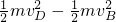
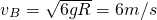
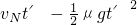


科目:高中物理 来源: 题型:
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com