
分析 地球自转周期为24h,根据ω=$\frac{2π}{T}$求解角速度.所需的向心力由F=mω2r求解.
解答 解:该同学随地球自转的周期为 T=24h=24×3600s
角速度ω=$\frac{2π}{T}$=$\frac{2×3.14}{24×3600}$rad/s≈7.2×10-5rad/s
所需的向心力 F=mω2r=mω2R地cos30°=50×(7.2×10-5)2×6.4×106×$\frac{\sqrt{3}}{2}$N≈1.4N
故答案为:7.2×10-5rad/s,1.4N.
点评 解决本题时要掌握角速度与周期的关系,向心力与角速度的关系,注意该同学圆周运动的半径不等于地球半径.


科目:高中物理 来源: 题型:多选题
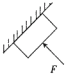 如图所示,一木块在垂直于倾斜天花板平面方向上的推力F的作用下处于静止状态,则下列判断中正确的是( )
如图所示,一木块在垂直于倾斜天花板平面方向上的推力F的作用下处于静止状态,则下列判断中正确的是( )| A. | 天花板对木块的摩擦力可能为零 | |
| B. | 天花板与木块间的弹力一定不为零 | |
| C. | 木块所受天花板的摩擦力随推力F的增大而变化 | |
| D. | 在逐渐增大推力F的过程中,木块将始终保持静止 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{m{v}^{2}}{GF}$ | B. | $\frac{m{v}^{4}}{GF}$ | C. | $\frac{2m{v}^{2}}{GF}$ | D. | $\frac{2m{v}^{4}}{GF}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
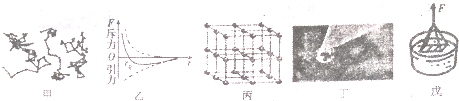
| A. | 甲图中微粒的运动就是物质分子的无规则热运动,即布朗运动 | |
| B. | 乙图中当两个相邻的分子间距离小于r0时,它们间相互作用只有斥力没有引力 | |
| C. | 丙图中食盐晶体中氯离子和钠离子都按一定规则排列,具有空间上的周期性 | |
| D. | 丁图中小草上的露珠呈球形的主要是液体表面张力的作用 | |
| E. | 戊图中洁净的玻璃板接触水面,要使玻璃离开水面,拉力F必须大于玻璃板的重力,其原因是分子之间存在引力 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 将重为20N的物体放在倾角为30°的粗糙斜面上,物体的一端与固定在斜面上的轻弹簧连接如图.若物体与斜面间最大静摩擦力为12N,物体静止时,弹簧的弹力( )
将重为20N的物体放在倾角为30°的粗糙斜面上,物体的一端与固定在斜面上的轻弹簧连接如图.若物体与斜面间最大静摩擦力为12N,物体静止时,弹簧的弹力( )| A. | 可以是22N,方向沿斜面向上 | B. | 可以是2N,方向沿斜面向上 | ||
| C. | 可以是2N,方向沿斜面向下 | D. | 可以是零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0.02s | B. | 0.1s | C. | 0.5s | D. | 2s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 振动图象从平衡位置开始计时 | B. | 2s末速度沿x轴负方向,加速度最大 | ||
| C. | 2s末速度最大,加速度为零 | D. | 1s末速度最大,加速度为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
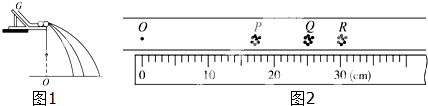
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{π}^{2}(8R+ct)^{3}}{2G{T}^{2}}$ | B. | $\frac{4{π}^{2}(8R+ct)^{3}}{G{T}^{2}}$ | C. | $\frac{{π}^{2}(2R+ct)^{3}}{2G{T}^{2}}$ | D. | $\frac{{π}^{2}(4R+ct)^{2}}{G{T}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com