
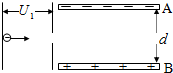
 如图所示,电子由静止开始经电压为U1的加速电场后进入AB极板组成的平行板电容器,若电子从AB极板正中间射入,电子正好能穿出电场.已知:电子的电量为e,质量为m,AB两极板间的电压为U2,距离为d,重力不计,求:
如图所示,电子由静止开始经电压为U1的加速电场后进入AB极板组成的平行板电容器,若电子从AB极板正中间射入,电子正好能穿出电场.已知:电子的电量为e,质量为m,AB两极板间的电压为U2,距离为d,重力不计,求:分析 (1)电子先在加速电场中加速,由动能定理可求其加速后的速度,
(2)根据牛顿第二定律求解加速度;
(3)电子进入偏转电场中做类平抛运动,由于电子正好能穿过电场,所以在偏转电场中的偏转的距离就是 $\frac{d}{2}$,由此可以求得极板的长度;
(4)电子正好能穿过电场偏转电场对电子做功为$\frac{q{U}_{2}}{2}$,根据动能定理求解电子穿出电场时的动能Ek.
解答 解:(1)对于电子在电场中加速过程,由动能定理得:
$e{U}_{1}=\frac{1}{2}m{{v}_{0}}^{2}$①
解得:${v}_{0}=\sqrt{\frac{2{U}_{1}e}{m}}$②
(2)在偏转电场中,由电子做类平抛运动,设加速度为a,极板长度为L,由于电子恰好射出电场,
根据牛顿第二定律得:$a=\frac{Ee}{m}$=$\frac{{U}_{2}e}{dm}$③
(3)根据类平抛运动的基本规律得:
L=v0t ④
$\frac{d}{2}=\frac{1}{2}a{t}^{2}$⑤
由②③④⑤解得:$L=d\sqrt{\frac{2{U}_{1}}{{U}_{2}}}$
(4)电子正好能穿过电场偏转电场,偏转的距离就是 $\frac{d}{2}$,由此对电子做功$\frac{q{U}_{2}}{2}$
此过程中,根据动能定理得:$\frac{q{U}_{2}}{2}={E}_{K}-\frac{1}{2}m{{v}_{0}}^{2}$⑤
①代人⑤中得:${E}_{K}=e({U}_{1}+\frac{{U}_{2}}{2})$
答:(1)经过加速电场后的速度v0为$\sqrt{\frac{2{U}_{1}e}{m}}$;
(2)电子在极板AB间的加速度a为$\frac{{U}_{2}e}{dm}$;
(3)极板AB的长度L为$d\sqrt{\frac{2{U}_{1}}{{U}_{2}}}$;
(4)电子穿出电场时的动能Ek为$e({U}_{1}+\frac{{U}_{2}}{2})$.
点评 电子先在加速电场中做匀加速直线运动,后在偏转电场中做类平抛运动,根据电子的运动的规律逐个分析即可,注意动能定理及平抛运动基本规规律在解题时的应用,难度适中.


科目:高中物理 来源: 题型:选择题
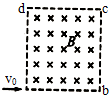 如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为υ0带电粒子从a点沿ab方向进人磁场,不计重力,则( )
如图所示,边长为L的正方形区域abcd内存在着匀强磁场.一个质量为m、电荷量为q、初速度为υ0带电粒子从a点沿ab方向进人磁场,不计重力,则( )| A. | 若粒子恰好从c点离开磁场,则磁感应强度B=$\frac{{m{υ_0}}}{2Lq}$ | |
| B. | 若粒子恰好从d点离开磁场,则磁感应强度B=$\frac{{m{υ_0}}}{Lq}$ | |
| C. | 若粒子恰好从bc边的中点离开磁场,则磁感应强度B=$\frac{{4m{υ_0}}}{5Lq}$ | |
| D. | 粒子从c点离开磁场时的动能大于从bc边的中点离开磁场时的动能 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 牛顿发现的万有引力定律,卡文迪许用实验方法测出万有引力常量的数值,从而使万有引力定律有了真正的实用价值 | |
| B. | 匀速圆周运动是速度大小不变的匀变速曲线运动,速度方向始终为切线方向 | |
| C. | 行星绕恒星运动轨道为圆形,则它运动的周期平方与轨道半径的三次方之比$\frac{{T}^{2}}{{R}^{3}}$=k常数,此常数的大小与恒星的质量和行星的速度有关 | |
| D. | 平抛运动中任意相等时间间隔内的速度变化量总是大小相等、方向竖直向下 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 杯子与地面和与地毯相互作用过程中动量的改变量相等 | |
| B. | 杯子与地面和与地毯相互作用过程中所受的合外力的冲量相等 | |
| C. | 杯子与地面和与地毯的相互作用力相等 | |
| D. | 杯子与地面和与地毯的相互作用时间相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | A点的电势是80V | |
| B. | 从A到B质子的电势能减少了30eV | |
| C. | 若以电子从A到B,电子的电势能减少30eV | |
| D. | AB两点的电势差为30V |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一个初速度为零的电子通过电压为4500V的电场加速后,从C点沿水平方向飞入场强为1.5×105V/m的匀强电场中,到达该电场中另一点D时,电子的速度方向与场强方向的夹角正好是120°,求C、D两点沿场强方向的距离.
如图所示,一个初速度为零的电子通过电压为4500V的电场加速后,从C点沿水平方向飞入场强为1.5×105V/m的匀强电场中,到达该电场中另一点D时,电子的速度方向与场强方向的夹角正好是120°,求C、D两点沿场强方向的距离.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
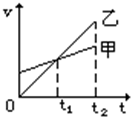 如图表示甲、乙两物体由同一地点同一时刻,向同一方向运动的速度图线,其中t2=2t1,则( )
如图表示甲、乙两物体由同一地点同一时刻,向同一方向运动的速度图线,其中t2=2t1,则( )| A. | 在t1时刻,甲物在前,乙物在后 | B. | 在t1时刻,甲、乙两物体相遇 | ||
| C. | 乙物的加速度大于甲物的加速度 | D. | 在t2时刻,甲、乙两物体相遇 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{\sqrt{gh}}}{3}$ | B. | 2$\sqrt{\frac{gh}{3}}$ | C. | $\frac{{2\sqrt{gh}}}{3}$ | D. | $\sqrt{\frac{gh}{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com