Question

14．如题图所示，在半径为a的圆柱空间中（图中圆为其横截面）充满磁感应强度大小为B的均匀磁场，其方向平行于轴线远离读者．在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架△DEF，其中心O位于圆柱的轴线上．DE边上S点（$\overline{DS}$=$\frac{1}{4}$L）处有一发射带电粒子的源，发射粒子的方向皆在题图中截面内且垂直于DE边向下．发射粒子的电量皆为q（＞0），质量皆为m，但速度v有各种不同的数值．若这些粒子与三角形框架的碰撞无能量损失（不能与圆柱壁相碰），电量也无变化，且每一次碰撞时速度方向均垂直于被碰的边．试问：
（1）带电粒子经多长时间第一次与DE边相碰？
（2）带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点？
（3）这些粒子中，回到S点所用的最短时间是多少？

Answer 1

分析 （1）经过半个周期粒子第一次与DE相碰，根据粒子做圆周运动的周期求出粒子的运动时间．
（2）S点发出的粒子最终又回到S点必须满足：要求此粒子每次与△DEF的三条边碰撞时都与边垂直，且能回到S点；粒子能绕过顶点与△DEF的边相碰；
（3）求出粒子做匀速运动转过的圆心角，然后由t=$\frac{θ}{2π}$求出粒子的运动时间．

解答 解：（1）粒子在磁场中做圆周运动的周期：T=$\frac{2πm}{qB}$，
粒子垂直与DE边射入磁场，在磁场中做匀速圆周运动，粒子转过半个圆周，即经过半个周期后第一次与DE相碰，
粒子在磁场中做圆周运动的周期：T=$\frac{2πm}{qB}$，
粒子第一次与DE相碰需要的时间：t=$\frac{1}{2}$T=$\frac{πm}{qB}$；
（2）带电粒子（以下简称粒子）从S点垂直于DE边以速度v射出后，
在洛伦兹力作用下做匀速圆周运动，其圆心一定位于DE边上，
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，
由牛顿第二定律得：qvB=m$\frac{{v}^{2}}{r}$，
解得：r=$\frac{mv}{qB}$…①
要求此粒子每次与△DEF的三条边碰撞时都与边垂直，且能回到S点，则R和v应满足以下条件：
（ⅰ）与边垂直的条件．
由于碰撞时速度v与边垂直，粒子运动轨迹圆的圆心一定位于△DEF的边上，
粒子绕过△顶点D、E、F时的圆弧的圆心就一定要在相邻边的交点（即D、E、F）上．
粒子从S点开始向右作圆周运动，其轨迹为一系列半径为R的半圆，
在SE边上最后一次的碰撞点与E点的距离应为r，所以$\overline{SE}$的长度应是R的奇数倍．
粒子从FD边绕过D点转回到S点时，情况类似，即$\overline{DS}$的长度也应是轨道半径的奇数倍．
取$\overline{DS}$=r₁，则当$\overline{DS}$的长度被奇数除所得的R也满足要求，即r=r_n=$\frac{\overline{DS}}{2n-1}$  n=1、2、3、…；
因此为使粒子与△DEF各边发生垂直碰撞，r必须满足下面的条件：r=r_n=$\frac{1}{2n-1}$$\frac{L}{4}$=$\frac{2a}{5（2n-1）}$   n=1、2、3、…②
此时：$\overline{SE}$=3$\overline{DS}$=（6n-3）r_n，n=1、2、3、…，$\overline{SE}$为r_n的奇数倍的条件自然满足．只要粒子绕过E点与EF边相碰，
由对称关系可知，以后的碰撞都能与△DEF的边垂直．
（ⅱ）粒子能绕过顶点与△DEF的边相碰的条件．
由于磁场局限于半径为a的圆柱范围内，如果粒子在绕E点运动时圆轨迹与磁场边界相交，
它将在相交点处以此时的速度方向沿直线运动而不能返回．所以粒子作圆周运动的半径R不能太大，
由图示可知，必须r≤$\overline{DM}$（△的顶点沿圆柱半径到磁场边界的距离，r=$\overline{DM}$时，
粒子圆运动轨迹与圆柱磁场边界相切），由给定的数据可算得：$\overline{DM}$=a-$\frac{8\sqrt{3}}{15}$a≈0.076a…③
将n=1，2，3，…，分别代入②式，得：
n=1 r₁=$\frac{2a}{5}$=0.400a n=2，r₂=$\frac{2a}{15}$≈0.133a，n=3 r₃=$\frac{2a}{25}$=0.080a，n=4  r₄=$\frac{2a}{35}$=0.057a，
由于R₁，R₂，R₃≥$\overline{DM}$，这些粒子在绕过△DEF的顶点E时，将从磁场边界逸出，
只有n≥4的粒子能经多次碰撞绕过E、F、D点，最终回到S点．
由此结论及①、②两式可得与之相应的速度：v_n=$\frac{qB}{m}$r_n=$\frac{qB}{m}$$\frac{2a}{5（2n-1）}$   n=4、5、6、…④
这就是由S点发出的粒子与△DEF的三条边垂直碰撞并最终又回到S点时，其速度大小必须满足的条件．
（3）这些粒子在磁场中做圆周运动的周期为：T=$\frac{2πm}{qB}$…⑤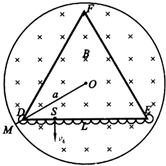
可见在B及$\frac{q}{m}$给定时T与v无关．粒子从S点出发最后回到S点的过程中，与△DEF的边碰撞次数愈少，
所经历的时间就愈少，所以应取n=4，如图所示（图中只画出在边框DE的碰撞情况），此时粒子的速度为v₄，
由图可看出该粒子的轨迹包括3×13个半圆和3个圆心角为300°的圆弧，所需时间为：
t=3×13×$\frac{1}{2}$T+3×$\frac{5}{6}$T=22T…⑥
将⑤式代入得：t=$\frac{44πm}{qB}$…⑦
答：（1）带电粒子经时间$\frac{πm}{qB}$第一次与DE边相碰；
（2）带电粒子速度v的大小取值为$\frac{qB}{m}$$\frac{2a}{5（2n-1）}$   n=4、5、6、…时可使S点发出的粒子最终又回到S点；
（3）这些粒子中，回到S点所用的最短时间是$\frac{44πm}{qB}$．

点评 本题考查了粒子咋磁场中的运动，分析清楚粒子运动过程是解题的关键，解题时要注意结合几何特性及半径与长度的关系；本题的难点在于先挖掘出粒子能回到S点需要满足的隐含条件以及考虑到粒子最终又回到S点时的多解性．