一物体质量为2kg，以4m/s的速度在光滑水平面上向左滑行，从某时刻起作用一向右的水平力，经过一段时间后，滑块的速度方向变为水平向右，大小为4m/s，在这段时间内水平力做功为（　　）

如图所示，一物块在与水平方向成θ角的拉力F的作用下，沿水平面向右运动一段距离l．则在此过程中，拉力F对物块所做的功为（　　）

关于物体机械能是否守恒的叙述，下列说法中正确的是（　　）

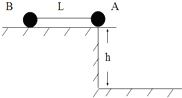A、B两球质量均为m，两球连线长为L，光滑水平面高为h，且L＞＞h，A球由桌边竖直下滑，落地后不再反弹．求：
（1）B球离开桌面时的速度；
（2）B和A落地点的水平距离．

事实上，地球围绕太阳运动的轨道是椭圆，并且太阳处在椭圆的一个焦点上．如图，已知太阳质量为M，半径为R，地球在近日点离太阳表面的距离为h₁，速度为v₁，在远日点地球离太阳表面的距离为h₂，万有引力常量为G．
求：（1）地球在远日点的速度为多少？
（2）地球在近日点、远日点的加速度各为多少？

如图所示，质点P以O为圆心、r为半径作逆时针匀速圆周运动，周期为了T，当质点P经过图中位置A时，另一质量为m、初速度为零的质点Q受到沿OA方向的拉力F作用从静止开始在光滑水平面上作直线运动，为使P、Q在某时刻速度相同，拉力F必须满足条件．

如图所示，用一根长杆和两个定滑轮的组合装置用来提升重物M，长杆的一端放在地上通过铰链连接形成转轴，其端点恰好处于左侧滑轮正下方0点处，在杆的中点C处拴一细绳，通过两个滑轮后挂上重物M．C点与O点距离为L，现在杆的另一端用力使其逆时针匀速转动，由竖直位置以角速度ω缓慢转至水平（转过了90°角），此过程中下述说法正确的是（　　）

如图所示的装置中，跨过右边定滑轮的A、B两球的质量都为m，且都绕竖直轴在同一水平面内做匀速圆周运动（圆锥摆运动），两球始终在同一直径的两端．跨过左边定滑轮的木块的质量为2m，则木块的运动情况是（　　）

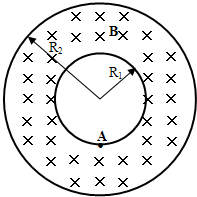据有关资料介绍，受控核聚变装置中有极高的温度，因而带电粒子将没有通常意义上的“容器”可装，而是由磁场约束带电粒子运动使之束缚在某个区域内．现按下面的简化条件来讨论这个问题：如图所示是一个截面为内径R₁=0.6m、外径R₂=1.2m的环状区域，区域内有垂直于截面向里的匀强磁场．已知氦核的荷质比

q

m

=4.8×10⁷C/kg，磁场的磁感应强度B=0.4T，不计带电粒子重力．
（1）实践证明，氦核在磁场区域内沿垂直于磁场方向运动，速度v的大小与它在磁场中运动的轨道半径r有关，试导出v与r的关系式．
（2）若氦核沿磁场区域的半径方向，平行于截面从A点射入磁场，画出氦核在磁场中运动而不穿出外边界的最大圆轨道示意图．
（3）若氦核平行于截面从A点沿各个方向射入磁场都不能穿出磁场外边界，求氦核的最大速度．

（2004?江苏模拟）1951年，物理学家发现了“电子偶数”，所谓“电子偶数”，就是由一个负电子和一个正电子绕它们的质量中心旋转形成的相对稳定的系统．已知正、负电子的质量均为m_e，普朗克常数为h，静电力常量为k．
（1）若正、负电子是由一个光子和核场相互作用产生的，且相互作用过程中核场不提供能量，则此光子的频率必须大于某个临界值，此临界值为多大？
（2）假设“电子偶数”中正、负电子绕它们质量中心做匀速圆周运动的轨道半径r、运动速度v及电子的质量满足量子化理论：
2m_ev_nr_n=n

h

2π

，n=1，2…，“电子偶数”的能量为正负电子运动的动能和系统的电势能之和，已知两正负电子相距为L时的电势能为Ep=-k

e2

L

．试求n=1时“电子偶数”的能量．
（3）“电子偶数”由第一激发态跃迁到基态发出光子的波长为多大？