
秘密★启用前
重庆一中高2009级高三下期5月月考
数 学(理科)试 题 卷 2009.5
数学试题共4页。满分150分。考试时间120分钟。
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
第Ⅰ卷(选择题,共 分)
分)
一、选择题:(本大题 10个小题,每小题5分,共50分)在每小题给出的四个选
1.已知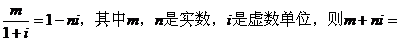 ( )
( )
A.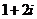 B.
B.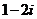 C.
C.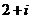 D.
D.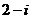
2.我市某中学高一年级有学生1200人,高二年级有学生900人,高三年级有学生
1500人,现用分层抽样的方法从中抽取一个容量为720的样本进行某项调查,则高
二年级应抽取的学生数为( )
A.180 B.240 C.480 D.720
3.曲线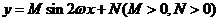 在区间
在区间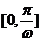 上截直线
上截直线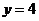 与
与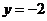 所得的
所得的
弦长相等且不为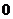 ,则下列描述中正确的是( )
,则下列描述中正确的是( )
A.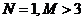 B.
B.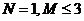 C.
C.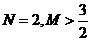 D.
D.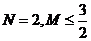
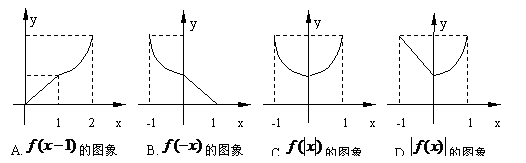 4.已知
4.已知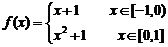 ,则下列函数的图象错误的是( )
,则下列函数的图象错误的是( )
5.下列四个条件中,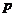 是
是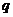 的必要不充分条件的是( )
的必要不充分条件的是( )
A.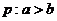 ,
,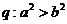 B.
B.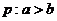 ,
,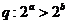
C.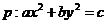 为双曲线,
为双曲线,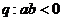 D.
D.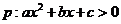 ,
,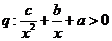
6.设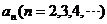 是
是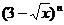 的展开式中
的展开式中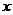 的一次项的系数,则
的一次项的系数,则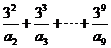
的值是( )
A.17 B.16 C.15 D.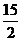
7.设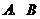 两地位于北纬
两地位于北纬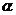 的纬线上,且两地的经度差为
的纬线上,且两地的经度差为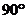 ,若地球的半径为
,若地球的半径为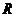 千
千
米,且时速为20千米的轮船从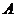 地到
地到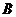 地最少需要
地最少需要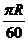 小时,则
小时,则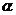 为( )
为( )
A.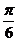 B.
B.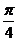 C.
C.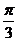 D.
D.
8.已知圆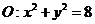 ,点
,点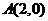 ,动点
,动点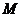 在圆上,则
在圆上,则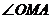 的最大值为( )A.
的最大值为( )A.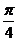 B.
B.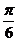 C.
C.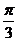 D.
D.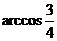
9.已知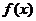 为定义在
为定义在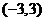 上的可导奇函数,且
上的可导奇函数,且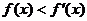 (其中
(其中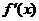 是
是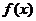 的导函数)对于
的导函数)对于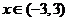 恒成立,则
恒成立,则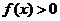 的解集为( )
的解集为( )
A.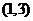 B.
B.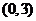 C.
C.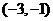 D.
D. 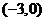
10.抛物线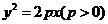 过焦点的弦
过焦点的弦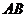 ,过该弦端点
,过该弦端点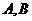 的两条切线的交点为
的两条切线的交点为
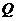 ,则
,则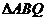 的面积的最小值为( )
的面积的最小值为( )
A.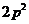 B.
B.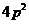 C.
C.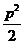 D.
D.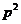
第Ⅱ卷(非选择题,共 分)
分)
卡相应位置上,只填结果,不要过程)。
二、填空题:(本大题5个小题,每小题5分,共25分)各题答案必须填写在答题
11.在等比数列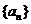 中,且
中,且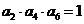 ,则
,则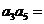 ___________。
___________。
12.已知函数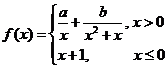 在
在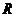 上连续,则
上连续,则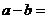 _________________。
_________________。
13.三棱锥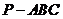 中,
中,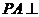 平面
平面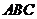 ,
,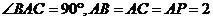 ,
,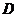 为
为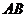
中点,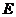 为
为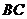 中点,则点
中点,则点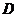 到直线
到直线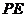 的距离等于________________。
的距离等于________________。
14.在同一平面内,已知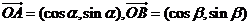 ,且
,且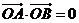 。若
。若
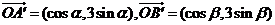 ,则
,则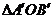 的面积等于________________。
的面积等于________________。
15.有机化学中一烷烃起始物的分子结构式是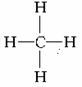 ,将其中的所有氢原子用甲基取代得到:
,将其中的所有氢原子用甲基取代得到: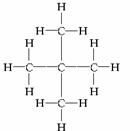 ,再将其中的12个氢原子全部用甲基代换,如此循环以至无穷,球形烷烃分子由小到大成一系列,则在这个系列中,由小到大第
,再将其中的12个氢原子全部用甲基代换,如此循环以至无穷,球形烷烃分子由小到大成一系列,则在这个系列中,由小到大第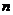 个分子中含有的碳原子的个数是____________________。
个分子中含有的碳原子的个数是____________________。
定的方框内(必须写出必要的文字说明、演算步骤或推理过程)。
三、解答题:(本大题6个小题,共75分)各题解答必须答在答题卷上相应题目指
16.(13分)在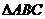 中,已知
中,已知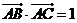 ,
,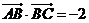 。
。
(1)求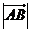 ;
;
(2)求证: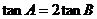 。
。
17.(13分)设点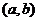 是区域
是区域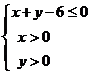 内的随机整点(整点是指横、纵坐标都
内的随机整点(整点是指横、纵坐标都
为整数的点)。
(1)已知关于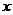 的一元二次函数
的一元二次函数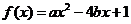 ,求函数
,求函数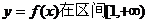 上是增函数的概率;
上是增函数的概率;
(2)设区域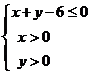 内的随机整点
内的随机整点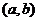 的横、纵坐标之和构成随机变量
的横、纵坐标之和构成随机变量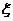 ,求
,求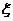 的分布列与期望。
的分布列与期望。
 18.(13分)如图,已知平行四边形
18.(13分)如图,已知平行四边形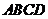 和矩形
和矩形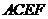 所在的平面互相垂直,
所在的平面互相垂直,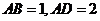 ,
,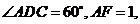
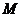 是线段
是线段
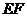 的中点。
的中点。
(1)求证: ;
;
(2)求二面角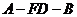 的大小;
的大小;
(3)设点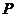 为一动点,若点
为一动点,若点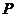 从
从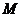 出发,
出发,
沿棱按照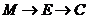 的路线运动到
的路线运动到
点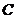 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥
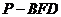 的体积的最小值。
的体积的最小值。
19.(12分)若存在实常数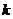 和
和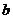 ,使得函数
,使得函数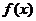 和
和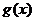 对其定义域上的任意实数
对其定义域上的任意实数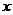
分别满足: 和
和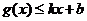 ,则称直线
,则称直线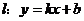 为
为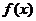 和
和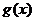 的“分
的“分
界直线”,已知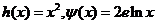 (其中
(其中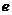 为自然对数的底数)。
为自然对数的底数)。
(1)求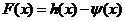 的极值;
的极值;
(2)函数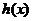 和
和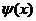 是否存在分界直线?若存在,求出此分界直线方程;若不存在,请说明理由。
是否存在分界直线?若存在,求出此分界直线方程;若不存在,请说明理由。
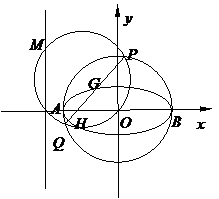 20.(12分)已知圆
20.(12分)已知圆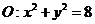 交
交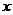 轴于
轴于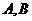 两点,
两点,
曲线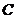 是以
是以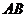 为长轴,直线
为长轴,直线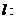
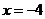 为准线的椭圆。
为准线的椭圆。
(1)求椭圆的标准方程;
(2)若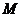 是直线
是直线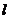 上的任意一点,以
上的任意一点,以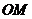 为直径的圆
为直径的圆
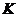 与圆
与圆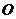 相交于
相交于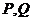 两点,求证:直线
两点,求证:直线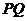 必过
必过
定点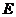 ,并求出点
,并求出点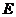 的坐标;
的坐标;
(3)如图所示,在(2)的条件下,若直线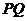 与椭圆
与椭圆
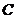 交于
交于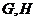 两点。试问在
两点。试问在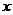 轴上是否存在定点
轴上是否存在定点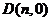 ,
,
使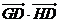 恒为定值
恒为定值 ?若存在,求出点
?若存在,求出点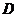 的坐标及
的坐标及
实数 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
21.(12分)设数列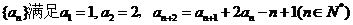 。
。
(1)求证: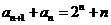 ;
;
1.C 2.A 3.A 4.D 5. D 6.B 7. B 8. A 9. B 10.D
11.  12. 2 13.
12. 2 13.  14.
14.  15.
15. 
16.解:(1)∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,  即
即 边的长度为
边的长度为 。
。
(2)由 ,得
,得 …………①
…………①
 ,即
,即 …………②
…………②
由①②得 ,由正弦定理
,由正弦定理 ,∴
,∴ ,即证。
,即证。
17. 解:(1)∵函数 的图象的对称轴为
的图象的对称轴为 要使
要使 在区间
在区间 上为增函数,当且仅当
上为增函数,当且仅当 且
且 。
。
依条件可知试验的全部结果为 ,即
,即
 共15个整点。
共15个整点。
所求事件为 ,即
,即 共5个整点,∴所求事件
共5个整点,∴所求事件
的概率为 。
。
(2)随机变量 的取值有:2,3,4,5,6。
的取值有:2,3,4,5,6。 的随机分布列为:
的随机分布列为:

2
3
4
5
6






随机变量 的期望
的期望 。
。
18.解法一:(1)易求 ,从而
,从而 ,由三垂线定理知:
,由三垂线定理知: 。
。
(2)法一:易求 由勾股定理知
由勾股定理知 ,设点
,设点 在面
在面 内的射影为
内的射影为 ,过
,过 作
作 于
于 ,连结
,连结 ,则
,则 为二面角
为二面角 的平面角。在
的平面角。在 中由面积法易求
中由面积法易求 ,由体积法求得点
,由体积法求得点 到面
到面 的距离是
的距离是
 ,所以
,所以 ,所以求二面角
,所以求二面角 的大小为
的大小为 。
。
法二:易求 由勾股定理知
由勾股定理知 ,过
,过 作
作 于
于 ,又过
,又过 作
作 交
交 于
于 ,连结
,连结 。则易证
。则易证 为二面角
为二面角 的平面角。在
的平面角。在 中由面积法易求
中由面积法易求 ,从而
,从而 于是
于是 ,所以
,所以
 ,在
,在 中由余弦定理求得
中由余弦定理求得 。再在
。再在 中由余弦定理求得
中由余弦定理求得 。最后在
。最后在 中由余弦定理求得
中由余弦定理求得 ,所以求二面角
,所以求二面角 的大小为
的大小为 。
。
(3)设AC与BD交于O,则OF//CM,所以CM//平面FBD,当P点在M或C时,三棱锥P―BFD的体积的最小。 。
。
解法二:空间向量解法,略。
19.解:(1)
 当
当 时,
时,
 当
当 时,
时, 此时函数
此时函数 递减;当
递减;当 时,
时, 此时函数
此时函数 递增;
递增; 当
当 时,
时, 取极小值,其极小值为0。
取极小值,其极小值为0。
(2)由(1)可知函数 和
和 的图像在
的图像在 处有公共点,因此若存在
处有公共点,因此若存在 和
和 的分界直线,则该直线过这个公共点。设分界直线的斜率为
的分界直线,则该直线过这个公共点。设分界直线的斜率为 则直线方程为
则直线方程为 即
即 由
由 可得
可得 当
当 时恒成立
时恒成立

 由
由 得
得 。
。
下面证明 当
当 时恒成立。
时恒成立。
令 则
则
当 时,
时, 。
。 当
当 时,
时, 此时函数
此时函数 递增;当
递增;当 时,
时, 此时函数
此时函数 递减;
递减; 当
当 时,
时, 取极大值,其极大值为0。
取极大值,其极大值为0。
从而 即
即 恒成立。
恒成立。
 函数
函数 和
和 存在唯一的分界直线
存在唯一的分界直线 。
。
20.解:(1)设椭圆的标准方程为 ,则:
,则:
 ,从而:
,从而: ,故
,故 ,所以椭圆的标准方程为
,所以椭圆的标准方程为 。
。
(2)设 ,则圆
,则圆 方程为
方程为 ,与圆
,与圆 联立消去
联立消去 得
得 的方程为
的方程为 ,过定点
,过定点 。
。
(3)将
 与椭圆方程
与椭圆方程 联立成方程组消去
联立成方程组消去 得:
得:
 ,设
,设 ,则
,则 。
。



 ,
,
所以 。
。
故存在定点 ,使
,使 恒为定值
恒为定值 。
。
21.解:(1)法一:数学归纳法;
法二:

所以 为首项为
为首项为 公比为2的等比数列,
公比为2的等比数列,
 ,即证。
,即证。
法三: ,两边同除以
,两边同除以 ,转化为叠加法求数列通项类型。
,转化为叠加法求数列通项类型。
(2)法一:容易证明 单调递增,
单调递增, 。由函数
。由函数 割线斜率与中点切线斜率的关系想到先证
割线斜率与中点切线斜率的关系想到先证 ,即证
,即证 ,即证
,即证

 。令
。令 下证
下证 。事实上,构造函数
。事实上,构造函数 ,则
,则
 ,
,
 ,所以
,所以 在
在 上单调递增,故
上单调递增,故 ,则
,则 ,即证
,即证 。
。
于是由 有
有 ,
,
(因为 )。
)。
法二:要证 ,即证
,即证

 ,联想到熟悉的不等式
,联想到熟悉的不等式 (证明如法一)。令
(证明如法一)。令 ,则
,则 ,即证
,即证
 ,下同方法一。
,下同方法一。
法三:联想到熟悉的不等式 (证略)。令
(证略)。令 ,则
,则
 ,即证
,即证
 而
而 ,但验算当
,但验算当 时
时 不成立。故单独验证
不成立。故单独验证 时原不等式成立,经验证成立。下用数学归纳法证
时原不等式成立,经验证成立。下用数学归纳法证 成立。
成立。
由 ,则
,则 ,作差有
,作差有 。
。
①当 时,
时, 成立。
成立。
②假设 时,
时, ,则
,则
当 时,
时, ,
,
下证 ,显然。所以,命题对
,显然。所以,命题对 时成立。综上①②即证。
时成立。综上①②即证。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com