练习册

  • 练习册
  • 试题
    界直线 .已知(其中为自然对数的底数). 【查看更多】

     

    题目列表(包括答案和解析)

    若存在实常数和，使得函数和对其定义域上的任意实数分别满足：和，则称直线为和的“隔离直线”．已知,（其中为自然对数的底数），根据你的数学知识，推断与间的隔离直线方程为                  .

    查看答案和解析>>

    已知函数其中为自然对数的底数

    （1）当时，求曲线在处的切线方程；

    （2）若函数为单调函数，求实数的取值范围；

    （3）若时，求函数的极小值。

     

     

    查看答案和解析>>

    已知函数其中为自然对数的底数， .

    (1)设，求函数的最值；

    (2)若对于任意的，都有成立，求的取值范围.

     

    查看答案和解析>>

    已知函数其中为自然对数的底数， .(Ⅰ)设，求函数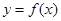的最值；（Ⅱ）若对于任意的，都有成立，求的取值范围.

    【解析】第一问中，当时，，．结合表格和导数的知识判定单调性和极值，进而得到最值。

    第二问中，∵，，      

    ∴原不等式等价于：,

    即, 亦即

    分离参数的思想求解参数的范围

    解：（Ⅰ)当时，，．

    当在上变化时，，的变化情况如下表：

     

    －

    ＋

     

    1／e

    ∴时，，．

    (Ⅱ)∵，，      

    ∴原不等式等价于：,

    即, 亦即．

    ∴对于任意的，原不等式恒成立,等价于对恒成立,

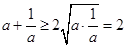    ∵对于任意的时, （当且仅当时取等号）．

    ∴只需，即，解之得或.

    因此，的取值范围是

     

    查看答案和解析>>

    已知函数（为自然对数的底数）

    （Ⅰ）若曲线在点处的切线平行于轴，求的值；

    （Ⅱ）求函数的极值；

    （Ⅲ）当时，若直线与曲线没有公共点，求的最大值.

     

    查看答案和解析>>

    1．C   2．A    3．A    4．D   5. D   6．B    7. B    8. A    9. B   10．D

    11. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     12.  2     13. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     14. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。    15. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    16．解：（1）∵高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

     ∵高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。, 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。边的长度为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    （2）由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………①

         高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………②

    由①②得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由正弦定理高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证。

    17． 解：（1）∵函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的图象的对称轴为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。要使高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在区间高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为增函数，当且仅当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    依条件可知试验的全部结果为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。共15个整点。

    所求事件为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。共5个整点，∴所求事件

    的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    （2）随机变量高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的取值有：2，3，4，5，6。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的随机分布列为：

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 

    2

    3

    4

    5

    6

     

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    随机变量高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的期望高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    18．解法一：（1）易求高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，从而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由三垂线定理知：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    （2）法一：易求高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由勾股定理知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，设点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在面高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。内的射影为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，过高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，连结高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为二面角高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的平面角。在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中由面积法易求高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由体积法求得点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。到面高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的距离是

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以求二面角高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的大小为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    法二：易求高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由勾股定理知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，过高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又过高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。交高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，连结高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。则易证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为二面角高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的平面角。在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中由面积法易求高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，从而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中由余弦定理求得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。再在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中由余弦定理求得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。最后在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中由余弦定理求得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以求二面角高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的大小为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    （3）设AC与BD交于O，则OF//CM，所以CM//平面FBD，当P点在M或C时，三棱锥P―BFD的体积的最小。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    解法二：空间向量解法，略。

    19.解：（1）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。此时函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。递减；当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。此时函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。递增；高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。取极小值，其极小值为0。

    （2）由（1）可知函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的图像在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。处有公共点，因此若存在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的分界直线，则该直线过这个公共点。设分界直线的斜率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。则直线方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。可得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时恒成立

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    下面证明高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时恒成立。

    令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。此时函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。递增；当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。此时函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。递减；高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。取极大值，其极大值为0。

    从而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。恒成立。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。存在唯一的分界直线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    20．解：（1）设椭圆的标准方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则：

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，从而：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,所以椭圆的标准方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    （2）设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则圆高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,与圆高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。联立消去高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，过定点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    （3）将高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。与椭圆方程高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。联立成方程组消去高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得：

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    故存在定点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，使高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。恒为定值高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    21．解：（1）法一：数学归纳法；

    法二：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为首项为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。公比为2的等比数列，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证。

    法三：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，两边同除以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，转化为叠加法求数列通项类型。

    （2）法一：容易证明高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。单调递增，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。由函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。割线斜率与中点切线斜率的关系想到先证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。下证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。事实上，构造函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上单调递增，故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    于是由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    （因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。）。

    法二：要证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，联想到熟悉的不等式高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。（证明如法一）。令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ，即证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，下同方法一。

    法三：联想到熟悉的不等式高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。（证略）。令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，但验算当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。不成立。故单独验证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时原不等式成立，经验证成立。下用数学归纳法证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。成立。

    由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，作差有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

    ①当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。成立。

    ②假设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    下证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，显然。所以，命题对高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时成立。综上①②即证。

     

     

     


    同步练习册答案