|
试题详情
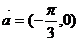 平移,所得曲线的一部分如图所示,则ω, 平移,所得曲线的一部分如图所示,则ω, 试题详情
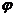 的值分别是( ) 的值分别是( ) 试题详情
A.1, B.1,- B.1,- 试题详情
C.2, D.2,- D.2,- 试题详情
8.已知向量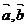 满足 满足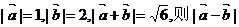 等于 ( ) 等于 ( ) 试题详情
试题详情
9.已知实数a,b满足等式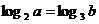 ,下列五个关系式:①1<a<b;②1<b< a;③b< a<1;④a<b<1;⑤a=b,其中不可能成立的关系有 ( ) ,下列五个关系式:①1<a<b;②1<b< a;③b< a<1;④a<b<1;⑤a=b,其中不可能成立的关系有 ( ) A.4 B.3 C.2 D.1 试题详情
10.下列函数既是奇函数,又在区间[-1,1]上单调递减的是 ( ) 试题详情
A. B. B. 试题详情
C.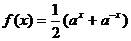 D. D. 试题详情
11.在△OAB中,O为坐标原点,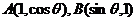 ,其中 ,其中 ,则当△OAB ,则当△OAB 的面积达到最小时,θ的值 ( ) 试题详情
试题详情
试题详情
A.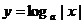 B. B. 试题详情
C. D. D. 第Ⅱ卷(共90分) 注意事项: 试题详情
试题详情
试题详情
二、填空题:本大题共4小题,每小题4分,共16分。答案须填在题中横线上。 13.已知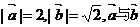 的夹角45°,要使 的夹角45°,要使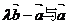 垂直,则λ= . 垂直,则λ= . 试题详情
试题详情
15.某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10千米处建仓库,这两项费用这两项费用y1和y2分别为2万元和8万元。那么,英才要使这两项费用之和最小,仓库应建在离车站
千米处。 试题详情
16.半径为r的圆的面积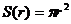 ,周长C(r)=2 ,周长C(r)=2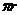 ,若将r看作是(0,+∞)上的变量,则 ,若将r看作是(0,+∞)上的变量,则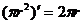 ……………………………………………………① ……………………………………………………① ①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数。 对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于 ①的式子:
……………………………………② ②式可用语言表述为:
试题详情
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
试题详情
在△ABC中,角A、B、C所对边分别为a、b、c,已知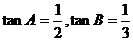 ,且最长边边长为1。 ,且最长边边长为1。 求:(Ⅰ)角C的大小; (Ⅱ)△ABC最短边的长。 试题详情
试题详情
已知向量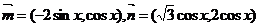 ,定义函数 ,定义函数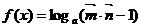 试题详情
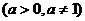 。 。
试题详情
(Ⅰ)求函数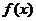 的最小正周期; 的最小正周期; 试题详情
(Ⅱ)求函数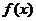 的最大值或最小值及此时对应的x的值; 的最大值或最小值及此时对应的x的值; 试题详情
(Ⅲ)确定函数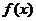 的单调递增区间。 的单调递增区间。 试题详情
试题详情
设数列{an}、{bn}满足: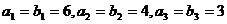 ,且数列 ,且数列 试题详情
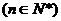 是等差数列,{bn-2}是等比数列。 是等差数列,{bn-2}是等比数列。
(Ⅰ)求数列{an}和{bn}的通项公式; 试题详情
(Ⅱ)是否存在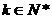 ,使 ,使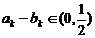 ,若存在,求出k;Y若不存在,说明理由。 ,若存在,求出k;Y若不存在,说明理由。 试题详情
试题详情
已知P:对任意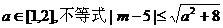 恒成立; 恒成立; 试题详情
Q:函数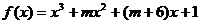 存在极大值和极小值。 存在极大值和极小值。 试题详情
求使“P且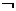 Q”为真命题的m的取值范围。 Q”为真命题的m的取值范围。 试题详情
21.(本小题满分12分) 某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示: 试题详情
 产品
产品
资源 甲产品 (每吨) 乙产品 (每吨) 资源限额 (每天) 煤(t) 9 4 360 电力(kw?h) 4 5 200 劳力(个) 3 10 300 利润(万元) 7 12 问:每天生产甲、乙两种产品各多少吨,获得利润总额最大? 试题详情
试题详情
对于数列{an},定义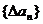 为数列{an}的一阶差分数列,其中 为数列{an}的一阶差分数列,其中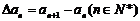 . . 试题详情
(Ⅰ)若数列{an}的通项公式 ,求 ,求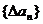 的通项公式; 的通项公式; 试题详情
(Ⅱ)若数列{an}的首项是1,且满足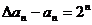 ,(1)证明数列 ,(1)证明数列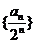 为等差数列;(2)求{an}的前n项和Sn。 为等差数列;(2)求{an}的前n项和Sn。 试题详情
一、选择题: 1―5:ACCCB 6―10:CDACD 11―12:BC 二、填空题: 13.2 14. 15.5
16.① 15.5
16.① ②球的体积函数的导数等于球的表面积函数 ②球的体积函数的导数等于球的表面积函数 三、解答题: 17.(本小题满分12分) 解:(I) ……………………2分 ……………………2分  ……………………4分 ……………………4分
 ……………………………………………………………………5分 ……………………………………………………………………5分 (II) 、B均为锐角且B<A 、B均为锐角且B<A 又C为钝角 ∴最短边为b……………………………………………………7分 由 ,解得 ,解得 ………………………………9分 ………………………………9分 又 …………………………12分 …………………………12分 18.(本小题满分12分) 解:(I) 
 ………………………………3分 ………………………………3分
故 …………………………………………………4分 …………………………………………………4分 (II)令 . . 若 时,当 时,当 时,函数 时,函数  …………………………………………………………6分 …………………………………………………………6分 若 时,当 时,当 时,函数 时,函数  …………………………………………………………8分 …………………………………………………………8分 (III)由 确定 单调递增的正值区间是 单调递增的正值区间是 ; ; 由 确定 单调递减的正值区间是 单调递减的正值区间是 ;………10分 ;………10分 综上,当 时,函数 时,函数 的单调递增区间为 的单调递增区间为 . . 当 时,函数 时,函数 的单调递增区间为 的单调递增区间为 .……12分 .……12分 注:①  的这些 的这些 等价形式中,以 最好用. 因为复合函数 最好用. 因为复合函数  的中间变量 的中间变量 是增函数,对求 是增函数,对求 的单调区间来说, 的单调区间来说,
只看外层函数 的单调性即可.否则,利用 的单调性即可.否则,利用 的其它形 的其它形 式,例如 求单调区间是非常容易出错的. 同学们可以尝试做一 求单调区间是非常容易出错的. 同学们可以尝试做一 下 的其它形式,认真体会,比较优劣! 的其它形式,认真体会,比较优劣! ②今后遇到求类似 的单调区间问题,应首先通过诱导公式将 的单调区间问题,应首先通过诱导公式将 转化为标准形 转化为标准形 式: (其中A>0,ω>0),然后再行求 (其中A>0,ω>0),然后再行求 解,保险系数就大了. 19.(本小题满分12分) 解:(I)由已知 ……………………1分 ……………………1分  …………3分 …………3分 由已知 ∴公差d=1…………………………………………………………4分 
 ……………………………………………………6分 ……………………………………………………6分
(II)设 …………………………7分 …………………………7分 当 时, 时, 是k的增函数, 是k的增函数, 也是k的增函数. 也是k的增函数.  ………………………………10分 ………………………………10分 又  不存在 不存在 ,使 ,使 …………………………………12分 …………………………………12分 20.(本小题满分12分) 解: 恒成立 恒成立 只需 小于 小于 的最小值…………………………………………2分 的最小值…………………………………………2分 而当 时, 时, ≥3……………………………………………4分 ≥3……………………………………………4分  ……………………………………………………6分 ……………………………………………………6分
 存在极大值与极小值 存在极大值与极小值
 有两个不等的实根…………………………8分 有两个不等的实根…………………………8分

 或 或 …………………………………………………………10分 …………………………………………………………10分
要使“P且 Q”为真,只需 Q”为真,只需 故m的取值范围为[2,6].…………………………………………………12分 21.(本小题满分12分) 解:设此工厂应分别生产甲、乙两种产品x吨、y吨,获得利润z万元………1分 依题意可得约束条件:

利润目标函数 …………(7分) …………(7分) 如图,作出可行域,作直线 ,把直线l向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时 ,把直线l向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时 取最大值.…………10分 取最大值.…………10分 解方程组 ,得M(20,24) ,得M(20,24) 故生产甲种产品20t,乙种产品24 t,才能使此工厂获得最大利润.…………12分 22.(本小题满分14分) 解:(Ⅰ)依题意 ∴ =5n-4 ……………………3分 (Ⅱ)(1)由 得
 即  ∴ ……………………6分 ……………………6分 即  ∵ ∴ 是以 是以 为首项, 为首项, 为公差的等差数列 ………………8分 为公差的等差数列 ………………8分 (2)由(1)得  ∴ ………………10分 ………………10分 ∴  ① ① ∴2 ② ② ①-②得 
= ∴ ………………14分 ………………14分
| | | 
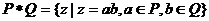 ,若P={-1,0,1},Q={-2,2},则集合
,若P={-1,0,1},Q={-2,2},则集合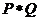 中元素的个数是 ( )
中元素的个数是 ( )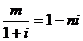 ,其中m,n是实数,是m+ni等于 ( )
,其中m,n是实数,是m+ni等于 ( )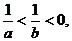 则下列不等式:①
则下列不等式:①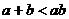 ②
②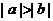 ③
③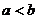 ④
④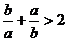 中,正确的不等式有 ( )
中,正确的不等式有 ( )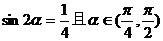 ,则
,则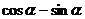 的值是 ( )
的值是 ( ) B.
B.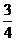 C.-
C.- D.-
D.-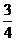
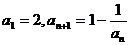 ,则a2007的值 ( )
,则a2007的值 ( )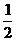 D.2
D.2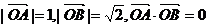 ,点C在∠AOB内,且∠AOC=45°,设
,点C在∠AOB内,且∠AOC=45°,设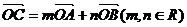 ,则
,则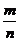 等于 ( )
等于 ( )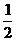 B.
B.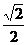 C.
C.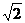 D.2
D.2