
日照实验高中2007年高考数学一轮复习周测七
时间 120分钟 满分 150分 2006.9.24
一、选择题
1、下列各式不能化为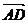 的是
的是
A
 B
B 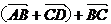
C 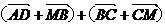 D
D 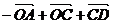
2、设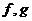 都是由A到A的映射(其中
都是由A到A的映射(其中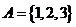 )其对应法则如下表:
)其对应法则如下表:
1
2
3
f
1
1
2
g
3
2
1
则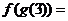
A
1 B
3、在四边形ABCD中, 其中
其中 不共线,则四边形ABCD是
不共线,则四边形ABCD是
A 梯形 B 矩形 C 菱形 D 正方形
4、设命题p,q为简单命题,则“p且q”为真是“p或q”为真的
A 充分不必要条件 B 必要不充分条件
C 充要条件 D 既不充分也非必要条件
5、 为不共线的向量,且
为不共线的向量,且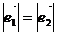 ,以下四个向量中模最小者为
,以下四个向量中模最小者为
A 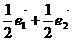 B
B 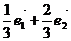 C
C 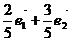 D
D
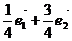
6、对于R上可导的任意函数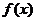 ,若满足
,若满足 ,则必有
,则必有
A  B
B 
C  D
D 
7、已知 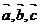 两两不共线的非零向量,且
两两不共线的非零向量,且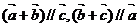 ,则下列结论中不正确的是
,则下列结论中不正确的是
A 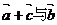 共线 B
共线 B 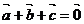 C
C 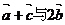 共线 D
共线 D 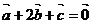
8、点P是曲线y=2-ln2x上任意一点,则点P到直线y=-x的最小距离为
A B C D
9、设函数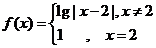 ,若关于
,若关于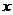 的方程
的方程
恰有5个不同的实数解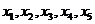 ,则
,则 等于
等于
A
0
B 2lg
10、设[x]表示不超过x的最大整数,又设x,y满足方程组 ,如果x不是整数,那么x+y是
,如果x不是整数,那么x+y是
A 在5与9之间 B 在9与11之间 C 在11与15之间 D 在15与16之间
11、在一次数学实验中, 运用图形计算器采集到如下一组数据:
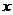
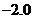

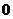
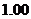

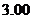
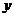
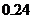
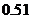
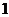
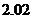
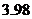
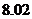
则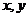 的函数关系与下列哪类函数最接近?(其中
的函数关系与下列哪类函数最接近?(其中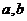 为待定系数)
为待定系数)
A 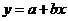 B
B 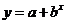 C
C 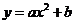 D
D 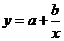
12、已知定义在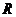 上的函数
上的函数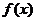 的图像关于点
的图像关于点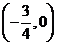 对称,且满足
对称,且满足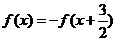 ,
,
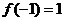 ,
,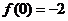 ,则
,则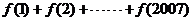 的值为
的值为
A 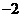 B
B 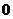 C
C 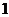 D
D 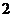
二、填空题
13、四边形ABCD中,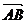 =
=
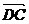 ,且|
,且|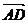 |=|
|=|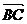 |,则四边形ABCD的形状是___________.
|,则四边形ABCD的形状是___________.
14、找一个非零函数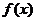 ,使
,使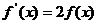 ,则
,则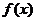 的解析式可以是_______________.
的解析式可以是_______________.
15、设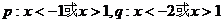 ,则
,则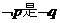 的____________________条件.
的____________________条件.
16、若含有集合A={1,2,4,8,16}中三个元素的A的所有子集依次记为B1,B2,B3,…,Bn(其中n∈N*),又将集合Bi(i=1,2,3,…,n)的元素的和记为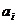 ,则
,则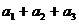
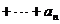 =
.
=
.
三、解答题
17、设直线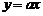
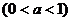 与抛物线
与抛物线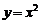 所围成的图形面积为S,它们与直线
所围成的图形面积为S,它们与直线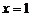 围成的面积为T, 若U=S+T达到最小值,求
围成的面积为T, 若U=S+T达到最小值,求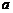 值
值
18、三个同学对问题“关于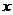 的不等式
的不等式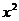 +25+|
+25+|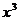 -5
-5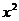 |≥
|≥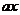 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数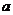 的取值范围”提出各自的解题思路。甲说:“只须不等式左边的最小值不小于右边的最大值”;乙说:“把不等式变形为左边含变量
的取值范围”提出各自的解题思路。甲说:“只须不等式左边的最小值不小于右边的最大值”;乙说:“把不等式变形为左边含变量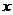 的函数,右边仅含常数,求函数的最值”;丙说:“把不等式两边看成关于
的函数,右边仅含常数,求函数的最值”;丙说:“把不等式两边看成关于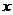 的函数,作出函数图像”。请你参考他们的解题思路,求出实数
的函数,作出函数图像”。请你参考他们的解题思路,求出实数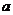 的取值范围。
的取值范围。
19、甲、乙两公司生产同一种产品,经测算,对于函数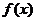 、
、 及任意的
及任意的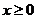 ,当甲公司投入
,当甲公司投入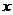 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于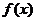 万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入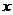 万元作宣传时,若甲公司投入的宣传费小于
万元作宣传时,若甲公司投入的宣传费小于 万元,则甲公司有失败的风险,否则无失败风险.
万元,则甲公司有失败的风险,否则无失败风险.
(Ⅰ)试解释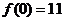 、
、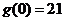 的实际意义;
的实际意义;
(Ⅱ)当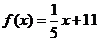 ,
,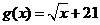 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
20、设f(x)=ln(x+m),
x [2-m, +
[2-m, +
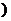 , x=
, x= 是方程f(x)=x的一根.
是方程f(x)=x的一根.
(1)求f(x)-2x的最大值;
(2)定理: 设f(x)定义域为[2-m, +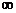
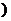 , 对任意[a, b]
, 对任意[a, b]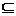 [2-m, +
[2-m, +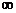
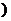 , 存在x
, 存在x
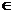 [a, b],
[a, b],
使等式f(b)-f(a)=(b-a) ? f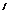 (x
(x ). 求证: 方程f(x)=x有唯一解x=
). 求证: 方程f(x)=x有唯一解x= .
.
21、在三角形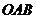 中,已知
中,已知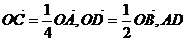 与
与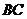 交于点
交于点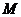 ,设
,设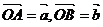 ,试以
,试以
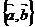 为基底表示
为基底表示 .
.
22、已知集合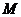 是满足下列性质的函数
是满足下列性质的函数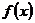 的全体:在定义域内存在
的全体:在定义域内存在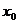 ,使得
,使得 成立.
成立.
(1)函数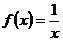 是否属于集合
是否属于集合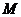 ?说明理由;
?说明理由;
(2)设函数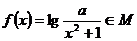 ,求
,求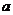 的取值范围;
的取值范围;
(3)设函数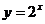 图象与函数
图象与函数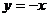 的图象有交点,证明:函数
的图象有交点,证明:函数 .
.
1-12题 AAAAA CDDCD BB
13、等腰梯形;14、 ;15、充分非必要;16、186
;15、充分非必要;16、186
17、
18、解:由 +25+|
+25+| -5
-5 |≥
|≥ ,而
,而 ,等号当且仅当
,等号当且仅当 时成立;且
时成立;且 ,等号当且仅当
,等号当且仅当 时成立;所以,
时成立;所以, ,等号当且仅当
,等号当且仅当 时成立;故
时成立;故 。
。
19、(Ⅰ) 表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费;
表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费; 表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费.
表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费.
(Ⅱ)设甲、乙公司投入的宣传费分别为 、
、 万元,当且仅当
万元,当且仅当 ①,
①,
且 ……②时双方均无失败的风险,
……②时双方均无失败的风险,
由①②得 易解得
易解得 ,
,
所以 ,故
,故 .
.
20、解:(1) 令g(x)=f(x)-2x=ln(x+m)-2x, 则g (x)=
(x)= -2
-2
∵x≥2-m ∴x+m≥2 ∴ ≤
≤ 从而g
从而g (x)=
(x)= -2≤
-2≤ -2<0
-2<0
∴g(x)在[2-m, +
 上单调递减 ∴x=2-m时,
上单调递减 ∴x=2-m时,
g(x)=f(x)-2x最大值=ln(2-m+m)-2(2-m)=ln2+
(2) 假设f(x)=x还有另一解x= (
(

 ) 由假设知
) 由假设知
 -
- =f(
=f( )-f(
)-f( )=f
)=f (x
(x )?(
)?( -
- ) x
) x
 [2-m, +
[2-m, +

故f (x
(x )=1, 又∵f
)=1, 又∵f (x
(x )=
)= ≤
≤ <1 矛盾
<1 矛盾
故f(x)=x有唯一解x=
21、
22、解:(1)若
 ,则在定义域内存在
,则在定义域内存在 ,
,
使得 ,∵方程
,∵方程 无解,
无解,
∴
 .
.
 ,
,
当 时,
时, , 当
, 当 时,由
时,由 ,
,
得 。
。
∴ .
.
 ,
,
又∵函数 图象与函数
图象与函数 的图象有交点,设交点的横坐标为
的图象有交点,设交点的横坐标为 ,
,
则 ,其中
,其中 ,
,
∴ ,即
,即 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com