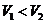|
试题详情
9. 在直二面角α―l―β中,直线a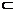 α, α, 试题详情
直线b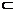 β,a、b与l斜交,则( ) β,a、b与l斜交,则( ) A.a不和b垂直,但可能a∥b B.a可能和b垂直,也可能a∥b C.a不和b垂直,a也不和b平行 D.a不和b平行,但可能a⊥b 试题详情
10. 不等式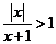 的解集为 ( ) 的解集为 ( ) 试题详情
A.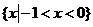 B. B.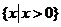 试题详情
C.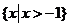 D. D.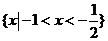 试题详情
11. 已知曲线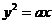 与其关于点(1,1)对称的曲线有两个不同的交点A、B,如果过这两个交点的直线的倾斜角是 与其关于点(1,1)对称的曲线有两个不同的交点A、B,如果过这两个交点的直线的倾斜角是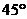 ,则实数a的值是 ( ) ,则实数a的值是 ( ) 试题详情
A.1
B.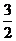 C.2
D.3
C.2
D.3 试题详情
试题详情
二、填空题:本大题共4小题,每小题4分,共16分.将答案填在题中的横线上.
试题详情
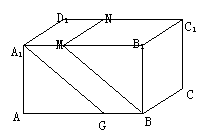 14. 如图,在长方体 14. 如图,在长方体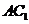 中,分别过BC和A1D1的两 中,分别过BC和A1D1的两
个平行平面如果将长方体分成体积相等的三个部分, 试题详情
那么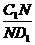 的值为 . 的值为 . 试题详情
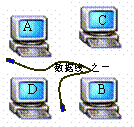 15. 如图,要用三根数据线将四台电脑A、B、C、D连接起来以实现资源共享,则不同的连接方案共有 种(用数字作答). 15. 如图,要用三根数据线将四台电脑A、B、C、D连接起来以实现资源共享,则不同的连接方案共有 种(用数字作答).
试题详情
16. 某种汽车安全行驶的稳定性系数μ随使用年数t的变 化规律是μ=μ0e-λt,其中μ0、λ是正常数.经检测,当t=2 试题详情
时,μ=0.09μ0,则当稳定系数降为0.50μ0时,该种汽车的使 试题详情
用年数为 (结果精确到1,参考数据:lg2=0.3010,lg3=0.4771). 试题详情
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17. (理科)已知△ABC内接于单位圆,且(1+tanA)(1+tanB)=2, (1)求证:内角C为定值; (2)求△ABC面积的最大值. 试题详情
(文科)已知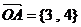 , ,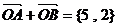 . . 试题详情
试题详情
试题详情
试题详情
18. 在一次历史与地理两科的联合测试中,备有6道历史题,4道地理题,共10道题以供选择,要求学生从中任意抽取5道题目作答,答对4道或5道可被评为良好。学生甲答对每道历史题的概率为0.9,答对每道地理题的概率为0.8. (1)求学生甲恰好抽到3道历史题,2道地理题的概率; 试题详情
(2)若学生甲恰好抽到3道历史题,2道地理题,则他能被评为良好的概率是多少?(精确到0.01) 试题详情
19. 如图,已知在 中, 中,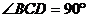 ,BC=CD=1, ,BC=CD=1,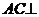 平面BCD, 平面BCD,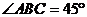 ,E是AB的中点. ,E是AB的中点. (1)求直线BD和CE所成的角; (2)求点C到平面ABD的距离; 试题详情
(3)若F是线段AC上的一个动点,请确定点F的位置,使得平面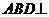 平面DEF. 平面DEF. 试题详情
试题详情
20. 已知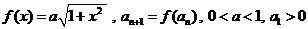 . . 试题详情
(1)求证:过曲线 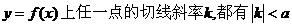 ; ; 试题详情
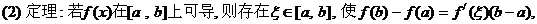 据此证明: 据此证明: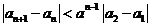 . .
试题详情
试题详情
试题详情
试题详情
22.(理科) 已知奇函数f(x),偶函数g(x)满足f(x)+ g(x)=ax(a>0且a≠1). (1)求f(x)、g(x)的表达式; 试题详情
试题详情
(3)令函数h(a)=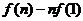 ,当 ,当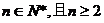 ,求函数h(a)的单调区间. ,求函数h(a)的单调区间. 试题详情
(文科)已知函数 . . 试题详情
试题详情
(2)在(1)的条件下,当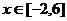 时, 时, <2|c|恒成立,求c的取值范围. <2|c|恒成立,求c的取值范围. 试题详情
一 、选择题 1.C.
2.A. 3.A. 4.A. 5.A.
6.C. 7.A. 8.A. 9.C.
10.D. 11.C.12.D. 一、
填空题 13. . 14.2. 15.16. 16.13. . 14.2. 15.16. 16.13. 三、解答题 17.(理科) (1)由(1+tanA)(1+tanB)=2,得 tanA+tanB=1-tanAtanB, 即tan(A+B)=1.
∵A、B为△ABC内角, ∴A+B= . 则 C= . 则 C= (定值). (定值). (2)已知△ABC内接于单位圆, ∴△ABC外接圆半径R=1. ∴由正弦定理得: , , , , . . 则△ABC面积S= = = = =
= = =
= = = . . ∵ 0<B< , ∴ , ∴ . . 故 当 时,△ABC面积S的最大值为 时,△ABC面积S的最大值为 . . (文科) (1) , ,  , , , , ,∴ ,∴  . .
∴ 向量 和 和 的夹角 的夹角 的大小为 的大小为 . . (2) . . 以 和 和 为邻边的平行四边形的面积 为邻边的平行四边形的面积 , , 据此猜想, 的几何意义是以 的几何意义是以 、 、 为邻边的平行四边形的面积. 为邻边的平行四边形的面积. 18. (1)学生甲恰好抽到3道历史题,2道地理题的概率为  . .
(2)若学生甲被评为良好,则他应答对5道题或4道题 而答对4道题包括两种情况:①答对3道历史题和1道地理(错一道地理题);②答对2道历史题和2道地理题(错一道历史题)。 设答对5道记作事件A; 答对3道历史题,1道地理题记作事件B; 答对2道历史题,2道地理题,记作事件C;  , ,  , ,  . . ∴甲被评为良好的概率为:  . . 19. (1)延长AC到G,使CG=AC,连结BG、DG,E是AB中点, . . 故直线BG和BD所成的锐角(或直角)就是CE和BD所成的角.  (2)设C到平面ABD的距离为h   20. (1) . . (2) 由(1)知: ,故 ,故 在 在 是增函数. 是增函数. 又 对于一切 对于一切 恒成立. 恒成立. 由定理知:存在 由(1)知:   由 的一般性知: 的一般性知: . . 21. (1)以 中点 中点 为原点, 为原点, 所在直线为 所在直线为 轴,建立平面直角坐标系,则 轴,建立平面直角坐标系,则 . .
设 ,由 ,由 得 得 ,此即点 ,此即点 的轨迹方程. 的轨迹方程. (2)将 向右平移一个单位,再向下平移一个单位后,得到圆 向右平移一个单位,再向下平移一个单位后,得到圆 , , 依题意有 . . (3)不妨设点 在 在 的上方,并设 的上方,并设 ,则 ,则 , , 所以 ,由于 ,由于 且 且 , , 故 . . 22.(理科)⑴ ∵f(x)+g(x)=ax,∴f(-x)+ g(-x)=a-x. ∵f(x)是奇函数,g(x)是偶函数,∴-f(x)+g(x)=a-x . ∴f(x)= ,g(x)= ,g(x)= . . ⑵  是R上的减函数, 是R上的减函数, ∴y=f -1(x)也是R上的减函数. 又 
⑶   
 n>2, n>2, 当 当 上是增函数. 上是增函数. 是减函数; 是减函数;
 上是减函数. 上是减函数. 是增函数. 是增函数.
(文科) (1)∵函数 在 在 和 和 时取得极值,∴-1,3是方程 时取得极值,∴-1,3是方程 的两根, 的两根, ∴ (2) ,当x变化时,有下表 ,当x变化时,有下表 x (-∞,-1) -1 (-1,3) 3 (3,+∞) f’(x) + 0 - 0 + f(x) ㄊ Max c+5 ㄋ Min c-27 ㄊ 而 时f(x)的最大值为c+54. 时f(x)的最大值为c+54. 要使f(x)<2|c|恒成立,只要c+54<2|c|即可. 当c≥0时c+54<2c, ∴c>54. 当c<0时c+54<-2c,∴c<-18. ∴c∈(-∞,-18)∪(54,+∞).
| 
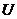 是实数集
是实数集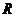 ,
,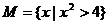 ,
,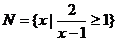 ,则图中阴影部分所表示的集合是 ( )
,则图中阴影部分所表示的集合是 ( )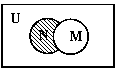 A.
A.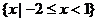 B.
B.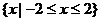
 D.
D.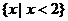
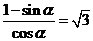 ,则
,则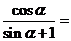 ( )
( )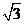 B.
B.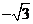 C.
C.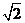 D.
D. 
 上逆时针旋转
上逆时针旋转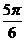 弧度到达Q点,则Q点的坐标是 ( )
弧度到达Q点,则Q点的坐标是 ( )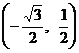 . B.
. B.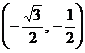 . C.
. C.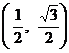 . D.
. D.
 A.
A.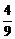 B.
B.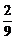 C.
C.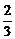 D.
D.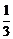
 绕点
绕点 顺时针旋转
顺时针旋转 ,再向上平移1个单位所得直线
,再向上平移1个单位所得直线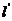 与圆
与圆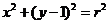 相切,则
相切,则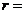 ( )
( )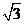 B.
B.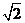 C.
C.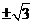 D.
D.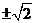
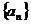 中,
中,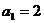 ,其前
,其前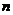 项和为
项和为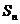 .当
.当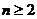 ,
, 时,
时,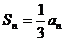 ,则
,则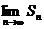 等于 ( )
等于 ( )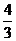 C.
C. D.3
D.3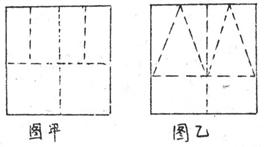 8. 将一边长为
8. 将一边长为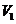 .若将同样的正方形纸片按照图乙中虚线所示的方法剪开后拼接为一正四棱锥,设其体积为
.若将同样的正方形纸片按照图乙中虚线所示的方法剪开后拼接为一正四棱锥,设其体积为 .则
.则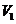 和
和 的大小关系
的大小关系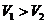 B.
B.