
2005―2006学年度上学期末部分学校毕业年级
调研测试二(课改区)
武汉市教育科学研究院命题
第Ⅰ卷(选择题,共17小题51分)
一、 判断题(本题共5小题,每小题3分,共15分)
1.方程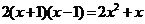 是一元二次方程.
是一元二次方程.
2.点A(-2,3)在第二象限.
3.tan30°= cot60°.
4.如果直线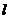 上有一点P到圆心O的距离等于圆的半径,那么直线
上有一点P到圆心O的距离等于圆的半径,那么直线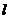 与⊙O相切.
与⊙O相切.
5.长度相等的两个半圆弧是等弧.
下列各题均有四个备选答案,其中有且只有一个答案是正确的,请在答题卡上把正确答案的代号涂黑。
二、选择题(本题共12小题,每小题3分,共36分)
6.一元二次方程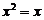 的根是( )
的根是( )
A.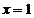 B.
B.
C. D.
D.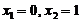
7.函数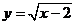 中自变量
中自变量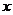 的取值范围是( )
的取值范围是( )
A. B.
B.
C.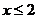 D.
D.
8.下列方程中,没有实数根的是( )
A. B.
B.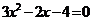
C.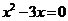 D.
D. 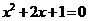
9.分解因式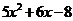 的结果是( )
的结果是( )
A.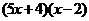 B.
B.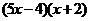
C.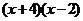 D.
D.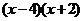
10.在Rt△ABC中,已知∠C = 90°,BC = 1,∠A = 30°,那么AC的长为( )
A.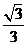 B.1 C.
B.1 C.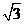 D.2
D.2
11.已知:如图A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD = 40°,那么∠AOC的度数为( )
A.80° B.70° C.50° D.40°
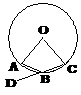
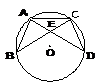
(第11题图) (第16题图)
12.已知等腰三角形的腰长为13 cm,底边长为10cm,那么它的外接圆的半径为( )cm
A.5 B.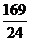 C.
C.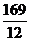 D.12
D.12
13.某山路的路面坡度(竖直高度与水平宽度的比)为1┱ ,沿此山路向上前进200米,则升高了( )米
,沿此山路向上前进200米,则升高了( )米
A.10 B.15 C.18 D.20
14.某公司的2003年产值为1650万元,2004年产值为2450万元,其增长率与上一个年度相同,那么2002年产值为( )万元
A.1650÷ B.1650÷
B.1650÷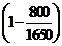
C.1650÷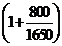 D.2450÷
D.2450÷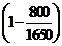
15.已知一元二次方程 的一根为
的一根为 ,另一根为
,另一根为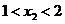 ,给出下列结论:①
,给出下列结论:①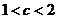 ;②
;②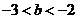 ;③
;③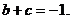 其中正确的结论的个数是( )
其中正确的结论的个数是( )
A.3 B.2 C.1 D.0
16.如图,⊙O中,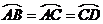 ,AB = 3,
,AB = 3,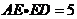 ,则CE的长为( )
,则CE的长为( )
A. B.
B.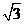 C.2 D.
C.2 D.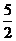
17.如图,已知AB是⊙O的直经,AC切⊙O于A点,且AB = AC,连结OC交⊙O于D点,连BD交AC于E,过D点作DF⊥AC于F点,连结OE交DF于P点。下列结论:①AF = CF;②DP = PF;③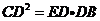 ;④EF┱DE = AD┱AC. 其中正确的结论是( )
;④EF┱DE = AD┱AC. 其中正确的结论是( )
A.①② B.①③
C.②③ D.②④
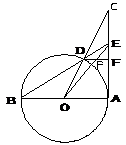
第Ⅱ卷(非选择题,共9小题69分)
三、填空题(本题共4小题,每小题3分,共12分)
18.已知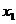 ,
,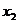 为一元二次方程
为一元二次方程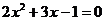 的两个实数根,那么
的两个实数根,那么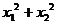 =__________.
=__________.
19.已知二元二次方程组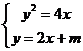 有两个不同的实数解,请你任意写出一个符合条件的
有两个不同的实数解,请你任意写出一个符合条件的 的值。
的值。 =______________.
=______________.
20.已知:如图,以Rt△ABC的斜边BC为直径作⊙O ,AD平分∠BAC交⊙O 于D,过D作⊙O 的切线交AC的延长线于点E,要使四边形BDEC为平行四边形,则△ABC中角或边应满足的条件是_______________(只须填一个).
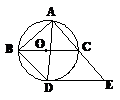

(第20题图) (第21题图)
21.已知:如图,AB是⊙O 的直径,弦CD交AB于P点,AP = 5,PB = 1,∠CPA = 45°,那么CD =__________.
四、解答题、证明题(本题共5小题,共57分)
22.(本题10分)实验得知:跳水运动员跳下的高度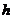 (米)与所用的时间
(米)与所用的时间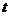 (秒)之间的函数关系式为:
(秒)之间的函数关系式为: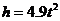 .
.
(1)若跳水运动员从10米高台上跳下,求跳水运动员从起跳到入水所用的时间;
(2)某著名跳水运动员能在0. 2秒内完成一个动作,并且在距水面3. 6米处开始入水准备不能做动作,那么该跳水运动员在10米高台跳水中能否完成5个动作?为什么?
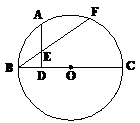
23.(本题10分)如图,已知⊙O中,BC是直径,D点为OB上任意一点(异于O、B),过D点作AD⊥BC,交⊙O于点A。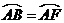 ,连结BF交AD于E点。
,连结BF交AD于E点。
(1)探究AE与BE的大小关系,并证明你的结论;
(2)当D为OC上任意一点(异于O、C),其它条件不变时,(1)中的结论是否仍然成立,画出图形并证明你的结论。

24.(本题10分)西部建设中,某工程队承包了一段72千米的铁轨的铺设任务,计划若干天完成,在铺设完一半后,增添工作设备,改进了工作方法,这样每天比原计划可多铺3千米,结果提前了2天完成任务。若按原计划操作,每天需各种费用1万元,而改进技术后每天需各种费用1. 2万元,问实际操作中,可比原计划节约多少元?
25.(本题12分)如图,已知平面直角坐标系中,点A(-1,a)、B(3,b)为两动点,其中A点在第二象限,B点在第一象限,以AB为直径画⊙M恰好经过O点.
(1)求证:ab = 3;
(2)是否存在实数a、b,使得△AOB的面积等于3,若存在,求a、b的值;若不存在,请说明理由.
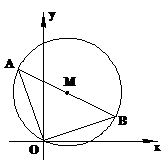
26.(本题15分)如图,在直角坐标系中,⊙O交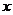 轴于A、B两点,交
轴于A、B两点,交 轴于C、D两点,A(-4,0),F为
轴于C、D两点,A(-4,0),F为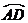 上一点,CF交AO于点E.
上一点,CF交AO于点E.
(1)若CF =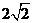 AF,求E点的坐标;
AF,求E点的坐标;
(2)连结BD并延长交AF的延长线于点G,连结EG,求证:EG⊥AB;

(3)如图,P为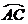 上的一个动点,AP的延长线交
上的一个动点,AP的延长线交 轴于M点,DP交
轴于M点,DP交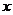 轴于点N. 当P在
轴于点N. 当P在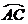 上运动时(不包括A、C点),给出下列两个结论:①
上运动时(不包括A、C点),给出下列两个结论:①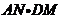 的值不变;②
的值不变;② 的值不变。其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变。其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com