
2007年聊城市莘县中考模拟考试三
数学试题
注意事项:
1.试题分值150分。考试时间120分钟。
2.本试卷分试题和答卷两部分。答案直接写在答卷上,考试结束时只交答卷,不交试题部分。
一、选择题(本大题共12个小题。每小题4分,共48分.在每小题给出的四个选项中,只有一个选项符合题目要求)
1.下列运算中不正确的是
A.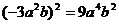 B.
B.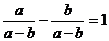
C.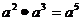 D.
D.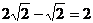
2.如果a≠0,且a、b互为相反数,则在下列各组数中,不是互为相反数的一组是
A.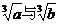 B.
B.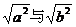
C.3a与3b D.a+1与b-1
3.如图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是
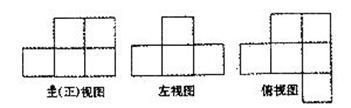
A.5个 B.6个 C.7个 D.8个
4.继短信之后,音乐类产品逐步成为我国手机用户的最爱和移动通信新的增长点.目前,中国移动彩铃用户数已超过40000000,占中国移动2亿余用户总数的近20%.40000000用科学记数法可表示为
A.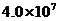 B.
B.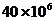 C.
C.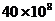 D.
D.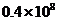
5.如图,AB∥CD,下列结论中正确的是
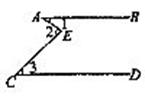
A.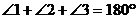 B.
B.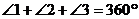
C.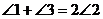 D.
D.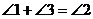
6.观察下图寻找规律,在“?”处填上数
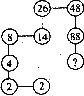
A.128 B.136 C.162 D.188
7.设一元二次方程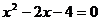 的两个实数根为
的两个实数根为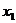 和
和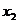 ,则下列结论正确的是
,则下列结论正确的是
A.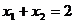 B.
B.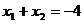
C.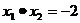 D.
D.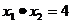
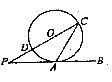
8.如图,过⊙O上的点A的切线AB与直径CD的延长线交于点P,若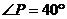 ,则∠BAC等于
,则∠BAC等于
A.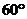 B.
B.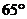
C.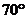 D.
D.
9.如图AD是△ABC的中线,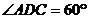 ,BC=4,把△ADC沿直线AD折叠后,点C落到
,BC=4,把△ADC沿直线AD折叠后,点C落到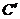 的位置上,那么
的位置上,那么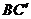 为
为
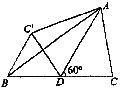
A.1 B.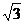 C.2 D.
C.2 D.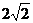
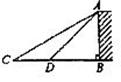
10.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角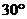 ,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为
,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为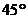 ,则建筑物AB的高度等于
,则建筑物AB的高度等于
A.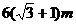 B.
B.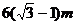
C.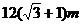 D.
D.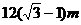
11.如图,点A是反比例函数图像上的一点,自点A向y轴作垂线,垂足为T,已知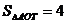 ,则此函数的表达式为
,则此函数的表达式为
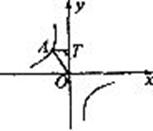
A.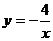 B.
B.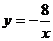
C.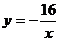 D.
D.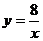
12.已知二次函数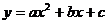 的图象如图所示,对称轴是
的图象如图所示,对称轴是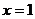 ,则下列结论中正确的是
,则下列结论中正确的是
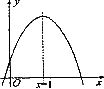
A.ac>0 B.b<0
C.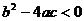 D.2a+b=0
D.2a+b=0
二、填空:(本题共5个小题,每小题4分,共20分)
13.函数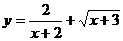 的变自量
的变自量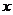 的取值范围是____________.
的取值范围是____________.
14.化简: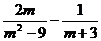 =____________.
=____________.
15.把一组数据中的每个数据都减去80,得一组新数据,若求得新一组数据的平均数是1.2,方差是4.4.则原来一组数据的平均数和方差分别为_____________
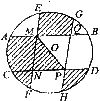
16.如图,将半径为2cm的⊙O分割成十个区域,其中弦AB、CD关于点O对称,EF、GH关于点O对称,连结PM,则图中阴影部分的面积是_______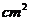 .(结果用
.(结果用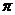 表示)
表示)
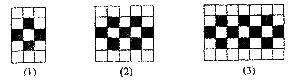
17.用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖______块,第n个图形中需要黑色瓷砖块(用含n的代数式表示).
三、解答题(本题共8个小题,共82分,解答应写出文字说明,详细解题过程)
18.(6分)解不等式组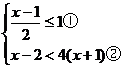 并写出不等式组的正整数解.
并写出不等式组的正整数解.
19.(9分)骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,下图表示一匹骆驼一天内体温随时间的变化情况:
根据该图回答下列问题:
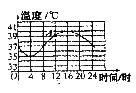

(1)图中A点所表示的实际意义是什么?
(2)在一天内,骆驼体温的最高与最低值相差多少度?
(3)在什么时间范围内骆驼的体温在上升?
20.(10分)小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字l,2,3,现将标有数字的一面朝下扣在桌子上.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张.
(1)用列表或画树状图等方法,列出小明和小亮抽得的卡片上所标数字的所有可能情况;
(2)计算小明和小亮抽得的两张卡片上的数字之和,如果和为奇数则小明胜,和为偶数则小亮胜,请判断游戏是否公平,并说明理由.
21.(10分)某商场销售某种商品,第一个月将此商品的进价提高25%作为销售价,共获利6000元.第二个月商场搞促销活动,将商品的进价提高10%作为销售价,第二个月的销售量比第一个月增加了80件,并且商场第二个月比第一个月多获利400元.问此商品的进价是多少元?商场第二个月共销售多少件?
22.(10分)如图,在△ABC中,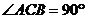 ,AC=2,BC=3,D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=
,AC=2,BC=3,D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=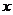
(1)当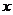 取何值时,四边形EACF是菱形?请说明理由;
取何值时,四边形EACF是菱形?请说明理由;
(2)当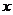 取何值时,四边形EACD的面积等于2
取何值时,四边形EACD的面积等于2
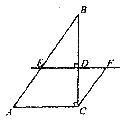
23.(10分)如图,⊙O的直径AB=4,∠ABC=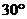 ,
,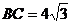 ,D是线段BC的中点.
,D是线段BC的中点.
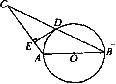
(1)试判断点D与QO的位置关系,并说明理由;
(2)过点D作DE上AC,垂足为点E,求证直线DE是GO的切线.
24.(12分)已知直线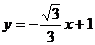 与x轴,
与x轴,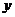 轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,
轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,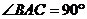 。且点P(1,
。且点P(1,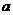 )为坐标系中的一个动点.
)为坐标系中的一个动点.
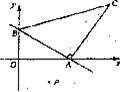
(1)求三角形ABC的面积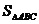 ;
;
(2)证明不论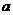 取任何实数,三角形BOP的面积是一个常数;
取任何实数,三角形BOP的面积是一个常数;
(3)要使得△ABC和△ABP的面积相等,求实数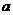 的值.
的值.
25.(15分)已知抛物线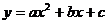 经过原点.与
经过原点.与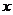 轴相交于另一点N,直线
轴相交于另一点N,直线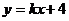 与坐标轴分别交于A、D两点,与抛物线相交于点B(1,m)、C(2,2)两点.
与坐标轴分别交于A、D两点,与抛物线相交于点B(1,m)、C(2,2)两点.
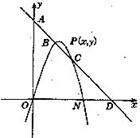
(1)求直线与抛物线的解析式;
(2)若(1)中抛物线在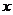 轴上方的部分有一动点P(
轴上方的部分有一动点P(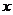 ,
,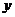 ),设
),设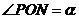 ,当
,当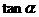 为何值时,△PON的面积有最大值?
为何值时,△PON的面积有最大值?
(3)若P点保持(2)中的运动路线,是否存在△PON,使其面积等于△OCN面积的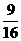 ?若存在,求出点P的位置;若不存在,请说明理由.
?若存在,求出点P的位置;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com