
2007年聊城市临清初三模拟考试(二)
数学试卷
亲爱的同学们,祝贺你顺利完成了第二轮复习,通过这次考试检验一下你复习的效果如何?请你在答卷之前仔细阅读以下说明:
1.试题由第Ⅰ卷和第Ⅱ卷组成,共6页。第Ⅰ卷为选择题,48分;第Ⅱ卷为非选择题,102分。共150分。考试时间为120分钟。
2.答第Ⅰ卷前,请你将姓名、准考证号、考试科目涂写在答题卡上。每小题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑。如需改动必须用橡皮擦干净,再改涂其它答案。
3.将第Ⅱ卷试题的答案宜接写在答卷上,考试结束后,答题卡、答卷一并交回。
4.可以使用科学计算器。
愿你放松心情,缜密思维,充分发挥,争取交一份圆满答卷。
第Ⅰ卷(选择题,共48分)
一、选择题(本题共12个小题,每小题4分。在每小题给出的四个选项中.只有一项符合题目要求)
1.计算 的值是
的值是
A.一9 B.
2.如图1是由一个正方体,将其沿一组对面的对角线切去一半,得到的一个立体图形,对于这一立体图形,其左视图、俯视图正确的一组是

A.a、b B.b、d C a、c D.a、d
3.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群之中,再第二次捕捞鱼共200条,有10条做了记号,则估计湖里有( )条鱼.
A.400 B.
4.如图2所示,若AB∥CD,∠ABE=120°, ∠DCE=35°,则∠BEC=
A.90° B.60°
C.95° D.85°

5.已知a>b>0,则下列不等式不一是成立的是
A. B.
B.
C.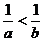 D.
D.
6.用边长为1的正方形纸板,做成一副七巧板,如图3,将它拱成“小天鹅”图案,如图4,其中阴影部分的面积为
A. B.
B.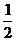 C.
C. D.
D.


7.甲、乙两同学从A地出发,骑自行车在同一条路上行驶,行驶到距A地18千米的B地,他们离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系的图象如图5所示,根据图中提供的信息,符合图象描述的说法是
A.甲在行驶过程中休息了一会儿
B.乙比甲先到达B地
C.乙在行驶过程中没有追上甲
D.甲的行驶速度比乙的行驶速度大

8.有一个商店把某件商品按进价加20%作为定价,可是总卖不出去;后来老板按定价减价20%,以96元出售,很快就卖掉了,则这次生意的盈亏情况为
A.赚6元 B.不亏不赚 C.亏4元 D.亏24
9.如图6,在正方形网格上有五个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有
A.1个 B.2个 C.3个 D.4个

10.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表:
跳高成绩(m)
1.50
1.55
1.60
1.65
1.70
1.75
跳高人数
1
3
2
3
5
1
这些运动员跳高成绩的中位数和众数分别是
A.1.65,1.70 B.1.70,
 11.如图7,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径
11.如图7,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径 ,AC=2,则cosB的值是
,AC=2,则cosB的值是
A. B.
B. C.
C. D.
D.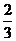
12.将正偶数按下表排成5列:
第一列
第二列
第三列
第四列
第五列
第一行
2
4
6
8
第二行
16
14
12
10
第三行
18
20
22
24
第四行
32
30
28
26
…
…
…
…
…
…
根据以上规律,2008应在
A.125行,3列 B.125行,2列 C .251行,5列 D.251行,3列
第Ⅱ卷(非选择题,共102分)
二、填空题(本题共5个小题,每小题4分,共20分。将最后结果直接填在答卷的相应位置)
 13.分解因式:
13.分解因式:
14.如图8是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是l3,小正方形的面积是l,直角三角形较长的直角边的长为a,较短的直角边的长为b,则a4+b4的值等于 .
15.小刚每天骑自行车上学都经过三个安装有红灯和绿灯的路口,假如每个路口红灯和绿灯亮的时间相同,那么小刚从家随时出发去学校,他至少遇到一次红灯的概率是 ,不遇红灯的概率是 .
16.在半径为
17.如图9,正华晚上由路灯A下的8处走到c处时,测得影子CD的长为

三、解答题(本题共8个小题.共82分。解答应写出必要的文字说明、证明过程或推演步骤)
18.(本题满分8分)化简求值: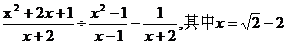 .
.
19.(本题满分8分)为了增强学生的法制观念,学校举办了一次法制知识竞赛,现将全校500名参赛学生的竞赛成绩(得分取整数)进行随机抽样,并绘制出统计图得到的频率分布表和频数分布直方图的一部分.
分组
频数
频率
0≤m<20
0
0
20≤m<40
40≤m<60
11
0.22
60≤m<80
23
0.46
80≤m<100
12
合计
1.00

(1)补全频率分布表;
(2)补全频数分布直方图;
(3)所抽查参赛学生中成绩中位数在第 组,全体参赛学生及格(不低于60分)的人数大约有多少人?
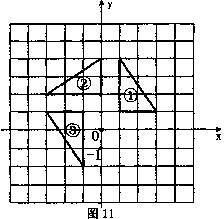
20.(本题满分10分)如图11,在平面直角坐标系中,三角形②③是由三角形①依次旋转后所得到的图形.
(1)在图中标出旋转中心P的位置,并写出它的坐标;
(2)在图上画出再次旋转后的三角形④.
21.(本题满分l0分)一水果经销商购进了A、B水果各10箱,分配给他的甲、乙两个零售店,预计每箱水果的赢利情况如下表:
A种水果/箱
B种水果/箱
甲 店
11元
17元
乙 店
9元
13元
(1)在甲、乙两店各分配10箱水果,且保证两店共赢利250元的情况下,请你给出分配方案;
(2)在甲、乙两店各分配10箱水果,且保证乙店赢利不小于l00元的情况下,问经销商至少应分配给甲店A种水果多少箱?此时经销商赢利多少元?
22.(本题满分10分)如图l2,CD是△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处.
(1)求∠A的度数;
(2)若 ,求△AEC的面积.
,求△AEC的面积.

23.(本题满分l2分)一条公路上有相距
(1)你能确定C在A什么方向吗?
(2)若此汽车由A驶向C需1小时,你能求出这辆汽车的行驶速度吗?(精确到0.1)
24.(本题满分l2分)两个全等的含30°,60°角的三角板ADE和三角板ABC,如图13所示放置,E、A、C三点在一条直线上,连接BD,取BD的中点M,连接ME、MC,试判断△EMC的形状,并说明理由.

25.(本题满分l4分)水产品公司购进一种鱼,其进货成本是每千克l0元,该公司对这一批鱼上市后的销售情况进行了跟踪调查,下表是销售量y(千克)与每千克销售价x(元)的部分对应值.
销售价z(元)
11
12
13
14
销售量y(千克)
190
180
170
160
(1)请你根据表中数据,确定哪种函数能表示Y与X的变化规律,写出Y与z的函数关系式;
(2)若销售利润为w元,请写出W与z之间的函数关系式;
(3)请你通过(2)中的函数关系式及其大致图象,帮助该公司确定这种鱼的销售单价范围,使这批鱼的利润不低于750元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com