
2007-2008学年度滨州市博兴第一学期期中教学质量检测
九年级数学试题
一、选择题(每小题3分,共45分。选出唯一正确答案的代号填在后面的答题栏内)
1.下列圆和正六边形中的各图,既可经过平移,又可经过旋转,由图形①得到②的是

A. B. C. D.
2.如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C、D两点。OH⊥AB于H,则图中相等的线段共有

A.1组 B.2组 C.3组 D.4组
3.如图,点A、C、B在上,若∠AOB=∠ACB=a,则a值为

A.135° B.120° C.110° D.100°
4.半径为5的⊙O,圆心在原点O,则点P(?3,4)与⊙O的位置关系是
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.不能确定
5.下列成语所描述的事件是必然发生的是
A.水中捞月 B.拔苗助长 C.守株待兔 D.瓮中捉鳖
6.对于上面选择题第5题,假定你不会做,于是随意猜测。能答对的概率是
A.
 B.
B. C.
C. D.
D.
2344
7.下列几个图形是国际通用的交通标志:其中不是中心对称图形的个数为

A.1 B.
8.在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。下列图案中,不是由同一个图形只通过旋转而构成的是
9.已知圆锥的底面半径为3,高为4,则圆锥的侧面积为
A.10 B.12
B.12 C.15
C.15 D.20
D.20
10.一个均匀的立方体六个面上分别标有数字1,2,3,4,5,6,下图是这个立方体表面的展开图。抛掷这个立方体,则朝上一面的数字恰好等于朝下一面的数字的 的概率是
的概率是

A.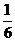 B.
B. C.
C. D.
D.
11.如下图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠A的度数是

A.72° B.63° C.54° D.36°
12.AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N,P、Q分别是弧AM、BM上一点(不与端点重合)。如果∠MNP=∠MNQ,则下面结论:

①∠l=∠2;②∠P+∠Q=∠180。;③∠Q=∠PMN:④PM=QM;⑤MN2=PN?QN。其中正确的是
A.①②③ B.①③⑤ C.④⑤ D.①②⑤
13.有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上,从中任意一张,则是数字3的概率是

A.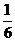 B.
B. C.
C. D.
D.
14.已知:如下图,⊙O的两条弦AE、BC相交于点D,连接AC、BE。若∠ACB=60°,则下列结论中正确的是

A.∠AOB=60° B.∠ADB=60° C.∠AEB=60° D.∠AEB=30°
15.正六边形的外接圆的半径与内切圆的半径之比为
A. B.
B. C.
C.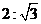 D.
D.
二、填空题(每小题4分,共20分)
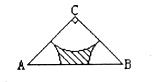
16.如下图,在Rt△ABC中,∠C=90°,CA=CB=2。分别以A、B、C为圆心,以 AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是
。
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是
。
17.如下图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是 cm。

18.同时掷二枚普通的骰子,数字和为7的概率为 。
19.用一条宽相等的足够长的纸条,打一个结,如下图甲所示,然后轻轻拉紧、压平就可以得到如图乙所示的正五边形ABCDE,其中∠BAC= 度。

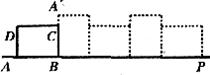
20.已知矩形ABCD的长AB=4,宽AD=3,按下图放置在直线AP上,然后不滑动地转动,当它转动一周时,顶点A所经过的路线长等于 。
三、解答题(共55分)
21.(6分)一张圆桌旁有四个座位,A先坐在一个固定座位上,然后B、C、D三人随机坐到其他三个座位上.求A与B不相邻而坐的概率。
22.(9分)如下图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是弧BD的中点,AB和DC的延长线交⊙O外一点E。

求证:BC=EC。
23.(9分)某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据:

(1)计算并完成表格:(精确到0.01)
转动转盘的次数
100
150
200
500
800
1000
落在“铅笔”的次数
68
111
136
345
564
701
落在“铅笔”的频率
(2)请估计,当 很大时,频率将会接近多少?
很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少(精确到l°)?
24.(9分)如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点。DE=DC,以D为圆心,以DB的长为半径画圆。
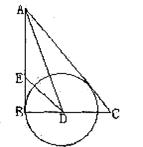
求证:(1)AC是⊙D的切线;(2)AB+EB=AC。
25.(10分)高致病性禽流感是比SARS病毒传染速度更快的传染病。
(1)某养殖场有8万只鸡,假设有1只鸡得了禽流感,如果不采取任何防治措施,那么,到第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依次类推,请问:到第四天,共有多少只鸡得了禽流感病?到第几天,该养殖场所有鸡都会被感染?
(2)为防止禽流感蔓延,政府规定:离疫点3千米范围内为扑杀区,所有禽类全部扑杀;离疫点3至5千米范同内为免疫区,所有的禽类强制免疫;同时,对扑杀区和免疫区内的村庄、道路实行全封闭管理。现有一条笔直的公路AB通过禽流感病区,如下图所示,O为疫点,在扑杀区内的公路CD长为4千米,问这条公路在该免疫区范围内有多少千米?

26.(12分)如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB。

(1)求证:AC是△BDE的外接圆的切线;
(2)若AD= ,AE=
,AE= ,求EC的长。
,求EC的长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com