
2008年5月无锡新区初中毕业升学二模试卷
数学
一. 细心填一填 (本大题共12小题,共15空,每空2分,共计30分)
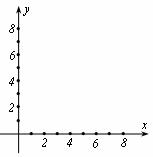
1.  的倒数是_____;25的算术平方根是_____。
的倒数是_____;25的算术平方根是_____。
2. 分解因式 = ____________ 。
= ____________ 。
3. 请写出一个正比例函数的解析式,并使其图像经过二、四象限______________。
4. 据报载,今年黄金周旅游刷新历史记录:太湖美景引来342万中外游客,这个数据用科学记数法记为_____________人。
5. 函数 中,自变量x的取值范围是________;函数y=
中,自变量x的取值范围是________;函数y= 中,自变量x的取值范围是____________。
中,自变量x的取值范围是____________。
6. 若一个多边形的每一个外角都等于30°,这个多边形的内角和是________。
7. 如图,在□ABCD中,对角线AC,BD相交于O,AC+BD=16,BC=6,则△AOD的周长为_________。

8. 如图,D、E分别是△ABC的边AC、AB上的点,请你添加一个条件: ,
使△ADE与△ABC相似。

9. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=

10.若两圆的半径是方程 的两个根,且圆心距等于7,则两圆的位置关系是___________________。
的两个根,且圆心距等于7,则两圆的位置关系是___________________。
11.甲、乙两人玩扑克游戏,每人手中有2、3、4、5各一张牌,两人同时出四张中的一张,如果两张牌对应的数的差的绝对值满足小于等于1,就说甲乙两人出牌默契。现任意找两人玩这个游戏,则“甲乙两人出牌默契”的概率为 。
12.如图,正方形ABCD的周长为
(1)出发后___________分钟时,甲乙两人第一次在正方形的顶点处相遇。
(2)如果用记号(a,b)的表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是______________。

二.精心选一选(本大题共有6小题,每小题3分,共计18分)
13.下列运算中,正确的是 ( )
A.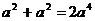 B.
B.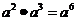 C.
C.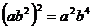 D.
D. 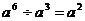
14.一次数学测试后,随机抽取九年级(1)班5名学生的成绩如下: 78,85,91,98,98,关于这组数据的错误说法是 ( )
A.极差是20 B.众数是
15.如图是几个小立方块所搭的几何体俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是 ( )
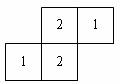
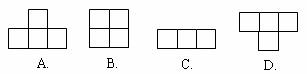
16.下列由正三角形和正方形拼成的图形中是轴对称图形不是中心对称图形是 ( )

A. B. C. D.
17.观察下列三角形数阵:则自上而下第60行的最后一个数是 ( )
A.3660 B.1830 C.1761 D.120

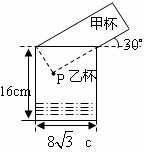
18.如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点 的距离是
(
)
的距离是
(
)
A.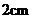 B.
B.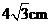 C.
C.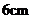 D.
D.
三.认真答一答(本大题共8小题,共计64分)
19.(每小题4分,共计12分)
(1)计算:(-2)3 + (2008-)0 - tan600
(2)解不等式组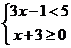
(3)将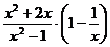 化简,并计算当x=-1时代数式的值.
化简,并计算当x=-1时代数式的值.
20.(本题6分)
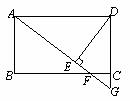
如图,在矩形ABCD中,F是BC上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC,根据上述条件,先请在图中找出一对全等三角形;并证明AF=BC。
21.(本题4分)
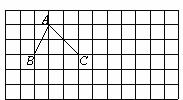
如图,已知△ABC,请在所给的方格纸(图中小正方形的边长为1个单位)内,按下列要求画出相应的图形.
(1)把△ABC先向下平移2个单位,再向右平移4个单位得到△DEF;
(2)将△DEF绕点D逆时针旋转90°得到△DE'F'.
22.(本题4分)
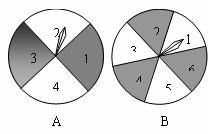
如图,转盘A被均匀地分成4等分,每份分别标上1,2,3,4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字. 有人为甲、乙两人设计了一个游戏,其规则如下:(1)同时自由转动转盘A、B;(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),把所指的两个数字相乘,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,则乙胜.你认为这样的规则是否公平?请通过计算说明;如果不公平,请你设计一个公平的规则.
23.(本小题8分)
甲、乙两同学做“射任意球”的游戏,他们商定:每人玩5局,每局在距球门25米处将足球射入空门,一次不进可以射第二次,依次类推,但最多只能射6次,当球射进后,该局结束,并记下射门次数;当6次都未射进,该局也结束,并记为“×”,两人5局射门进球情况如下:
第一局
第二局
第三局
第四局
第五局
甲
5次
×
4次
×
1次
乙
×
2次
4次
2次
×
(1)为了计算得分,双方约定:记“×”的该局为0分,其他局得分的计算方法要满足以下两个条件:①射门次数越多,得分越低;②得分为正数。请你按约定的要求,用公式或文字叙述的方式,选取其中的一种写出一个将其他局的射门次数n换算成得分M的具体方案;
(2)根据上述约定和你写出的方案,请你通过表格的方式,统计甲、乙两人的每局得分和平均分,并从平均分的角度来判断甲、乙两人谁的任意球射门技术更精湛。
24.(本小题6分)
如图,在平面直角坐标系中,M是X轴正半轴上一点,⊙M与X轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程x2-12x+27=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
(1)求⊙M的直径.(2)求 的值.(3)求直线ON的解析式.
的值.(3)求直线ON的解析式.

25.(本小题8分)
点O是△ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,如果DEFG能构成四边形。
(1)如图,当点O在△ABC内时,求证:四边形DEFG是平行四边形。
(2)当点O移动到△ABC外时,(1)的结论是否成立?画出图形并说明理由。
(3)若四边形DEFG为矩形,点O所在位置应满足什么条件?试说明理由。

26.(本小题8分)
无锡新区某电子公司根据市场需求,在一天内计划生产A、B两种型号的电子产品共52件,该公司所筹生产此电子产品的资金不少于2710元,但不超过2794元,且所筹资金全部用于生产此两型电子产品,所生产的此两型电子产品可全部售出,此两型电子产品的生产成本和售价如下表:

(1)该公司对这两型电子产品有哪几种生产方案?
(2)该公司如何生产能获得最大利润?
(3)根据市场调查,每件B型电子产品的售价不会改变,而每件A型电子产品的售价将会提高m元(m>40),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
27.(本小题8分)
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:

请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,
长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为 m,长方形框架ABCD的面积为S= (用含
m,长方形框架ABCD的面积为S= (用含 的代数式表示);当AB= m时, 长方形框架ABCD的面积S最大;
的代数式表示);当AB= m时, 长方形框架ABCD的面积S最大;
(3)在图案(3)中,如果铝合金材料总长度为 m, 设AB为
m, 设AB为 m,求出ABCD的面积S与
m,求出ABCD的面积S与 的函数关系式,并求出当AB为多少m时, 长方形框架ABCD的面积S最大.
的函数关系式,并求出当AB为多少m时, 长方形框架ABCD的面积S最大.
四.实践与探索(本大题共2小题,共计18分)
28.(本题8分)
原始问题:已知矩形A的长、宽分别是2和1,那么是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?
对上述问题,小明同学从“图形”的角度,利用函数知识给予了解决。
小明论证的过程开始是这样的:如果用x、y分别表示矩形的长和宽,那么矩形B满足x+y=6,xy=4。请你按照小明的论证思路完成后面的论证过程。
新的问题:已知矩形A的长和宽分别是2和1,那么是否存在一个矩形C,它的周长和面积分别是矩形A的周长和面积的一半?
小明认为这个问题是肯定的,你同意小明的观点吗?为什么?
29.(本小题10分)
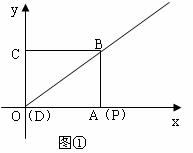
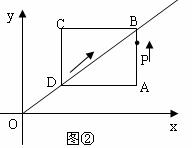
如图①,矩形ABCD的两条边在坐标轴上,点D与原点O重合,对角线BD所在的直线的函数关系式为y=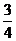 x,AD=8。矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒。
x,AD=8。矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒。
(1)求矩形ABCD 的周长。
(2)如图②,图形运动到第5秒时,求点P的坐标。
(3)设矩形运动的时间为t,当0≤t≤6时,点P所经过的路线是一条线段,请求出线段所在直线的函数关系式。
(4)当点P在线段AB或BC上运动时,过点P作x轴、y轴的垂线,垂足分别为E、F,则矩形PEOF是否能与矩形ABCD相似(或位似)?若能,求出t的值;若不能,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com