
2008年湖北省咸宁市初中毕业生学业考试
数学试卷
参考公式:抛物线y=ax2+bx+c( ,
, ,
, 是常数,a≠0)的顶点坐标是(
是常数,a≠0)的顶点坐标是( ).
).
一、精心选一选(本大题共8小题,每小题3分,共24分)每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题目后的括号内
1.-5的相反数是
A.5 B.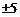 D.
D.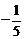
2.化简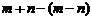 的结果为
的结果为
A.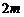 B.
B.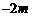 C.
C.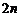 D.
D.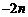
3.2008年北京奥运会火炬接力传递距离约为137 000千米,将137 000用科学记数法表示为
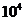 B. 137×
B. 137×
4.在Rt△ABC 中, ∠C=90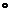 ,AB=4,AC=1,则
,AB=4,AC=1,则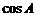 的值是
的值是
A.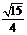 B.
B.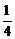 C.
C.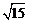 D.4
D.4
5. 下图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是
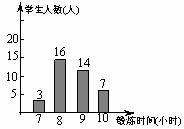
A.极差是3 B.中位数为8
C.众数是8 D.锻炼时间超过8小时的有21人
6.两个完全相同的长方体的长、宽、高分别为3、2、1,把它们叠放在一起组成一个新的长方体,在这些新长方体中,表面积最小值为
A.42
B.
7.下列说法:①对角线互相平分且相等的四边形是菱形; ②计算 的结果为1;
的结果为1;
③正六边形的中心角为60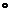 ; ④函数
; ④函数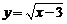 的自变量
的自变量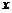 的取值范围是
的取值范围是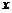 ≥3.
≥3.
其中正确的个数有
A.1个 B.2个 C.3个 D.4个
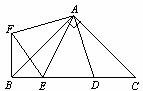
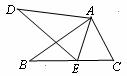
8.如图,在Rt△ABC 中,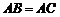 ,D、E是斜边BC上两点,且∠DAE=45°,将△
,D、E是斜边BC上两点,且∠DAE=45°,将△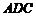
绕点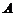 顺时针旋转90
顺时针旋转90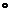 后,得到△
后,得到△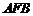 ,连接
,连接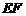 ,下列结论:
,下列结论:
①△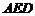 ≌△
≌△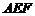 ; ②△
; ②△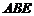 ∽△
∽△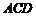 ;
;
③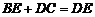 ; ④
; ④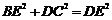
其中正确的是
A.②④; B.①④;
C.②③; D.①③.
二、细心填一填(本大题共8小题,每小题3分,满分24分)请把答案直接写在题中的横线上
9.跳远训练时,甲、乙两同学在相同条件下各跳10次,统计得,他们的平均成绩都是5.68,
甲的方差为0.3,乙的方差为0.4,那么成绩较为稳定的是 (填“甲”或“乙”).
10.如图,AB∥CD,∠C=65o,CE⊥BE ,垂足为E,则∠B的度数为 .
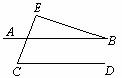
11.如图∠DAB=∠CAE,请补充一个条件: ,使△ABC∽△ADE.
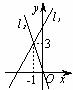
12.直线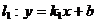 与直线
与直线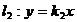 在同一平面直角坐标系中的图象如图所示,则关于
在同一平面直角坐标系中的图象如图所示,则关于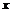 的不等式
的不等式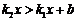 的解集为
.
的解集为
.
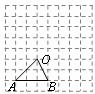
13.如图,在8×8的网格中,每个小正方形的顶点叫做格点,△OAB的顶点都在格点上,请在网格中画出△OAB的一个位似图形,使两个图形以O为位似中心,且所画图形与△OAB的位似比为2┱1.
14.抛物线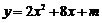 与
与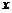 轴只有一个公共点,则
轴只有一个公共点,则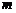 的值为 .
的值为 .
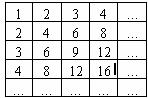
15.观察下表,依据表格数据排列的规律,数2 008在表格中出现的次数共有 次.
16.两个反比例函数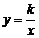 和
和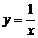 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在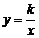 的图象上,PC⊥x轴于点C,交
的图象上,PC⊥x轴于点C,交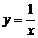 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交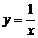 的图象于点B,当点P在
的图象于点B,当点P在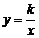 的图象上运动时,以下结论:
的图象上运动时,以下结论:
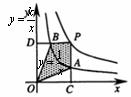
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;③PA与PB始终相等;
④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).
三、专心解一解(本大题共8小题,满分72分)请认真读题,冷静思考.解答题应写出文字说明、证明过程或演算步骤
17.(本题满分6分)
先化简,再求值: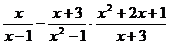 ,其中
,其中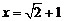 .
.
18.(本题满分8分)
A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运
19.(本题满分8分)
如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
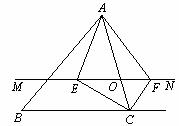
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
20.(本题满分9分)
有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.

(1)用画树形图或列表法表示抽取两张卡片可能出现的所有情况(卡片可用A、B、C、D表示);(2)分别求抽取的两张卡片上的算式都正确的概率和只有一个算式正确的概率.
21.(本题满分9分)
如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.
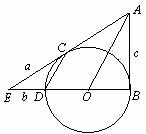
(1)试探究A E与⊙O的位置关系,并说明理由;
(2)已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,设计出计算⊙O的半径r的一种方案:
①你选用的已知数是 ;
②写出求解过程(结果用字母表示).
22.(本题满分10分)
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
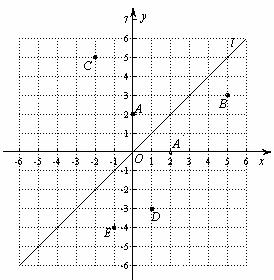
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点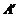 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点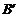 、
、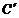 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:
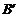 、
、 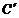 ;
;
归纳与发现:
运用与拓广:
(3)已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点 的坐标为
(不必证明);
的坐标为
(不必证明);
23.(本题满分10分)
“5?
(1) 请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C
D
总计
A
200吨
B
x吨
300吨
总计
240吨
260吨
500吨
(2) 设A、B两个蔬菜基地的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)
经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少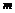 元(
元(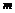 >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.
24.(本题(1)~(3)小题满分12分,(4)小题为附加题另外附加2分)
如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
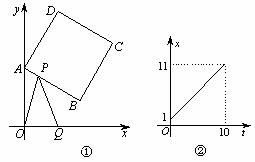
(1)当P点在边AB上运动时,点Q的横坐标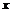 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(4)附加题:(如果有时间,还可以继续解答下面问题,祝你成功!)
如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com