
2008年北京市顺义区初三年级二模考试
数学试卷
一、选择题
1. 的绝对值是( )
的绝对值是( )
A.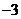 B.
B.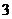 C.
C.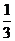 D.
D.
2.若分式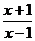 的值为0,则x的值是( )
的值为0,则x的值是( )
A.-1 B.
3.若反比例函数的图象经过点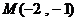 ,则反比例函数的解析式为( )
,则反比例函数的解析式为( )
A.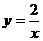 B.
B.  C.
C. 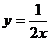 D.
D.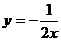
4.算式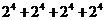 的结果是( )
的结果是( )
A.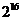 B.
B.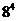 C.
C.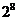 D.
D.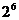
5.刘强同学为了调查全市初中生人数,他对自己所在城区人口和城区初中生人数作了调查:城区人口约3万,初中生人数约1200.全市实际人口约300万,为此他推断全市初中生人数约为12万.但市教委提供的全市初中生人数约为8万,与估计数据有很大偏差.请你用所学的统计知识,找出其中错误的原因是( )
A.样本不能估计总体 B.样本不具代表性、广泛性、随机性
C.市教委提供的数据有误 D.推断时计算错误
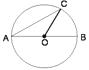
6.如图,AB是⊙O的直径,AC是弦,若AB=2, AC=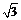 ,则∠AOC的度数是 ( )
,则∠AOC的度数是 ( )
A.120° B.130° C.140° D.150°
7.下面三张卡片上分别写有一个整式,把它们背面朝上洗匀,小明从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张.第一次抽取的卡片上的整式做分子,第二次抽取的卡片上的整式做分母,则能组成分式的概率是 ( )
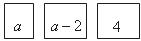
A.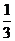 B.
B.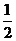 C.
C.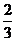 D.
D.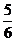
8.如图是一个经过改造的台球桌面的示意图,图中4个角上的阴影部分分别表示4个入球孔.如果1个球按图中所示的方向被击中(球可以经过多次反射,并且不会在台球桌中间停止),那么该球最后将落入的球袋是( )
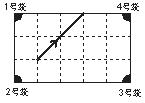
A.1号袋 B.2号袋 C.3号袋 D.4号袋
二、填空题(共4个小题,每小题4分,共16分)
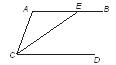
9.已知:如图,AB∥CD,CE平分∠ACD,交AB于点E,若∠A=110°,则∠BEC的度数是 .
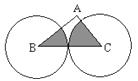
10.如图,在△ABC中,∠A=90 ,分别以B、C为圆心的两个等圆外切,两圆的半径都为
,分别以B、C为圆心的两个等圆外切,两圆的半径都为
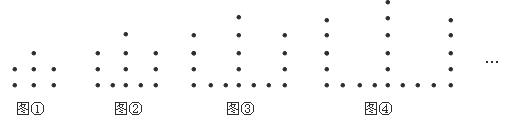
11.如图,图①,图②,图③,图④……是用围棋棋子摆成的一列具有一定规律的“山”字.则第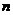 个“山”字中的棋子个数是
.
个“山”字中的棋子个数是
.
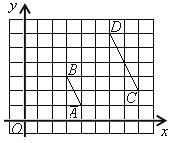
12. 线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(a,b),则直线OP与线段CD的交点的坐标为________________.
13.分解因式: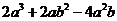 .
.
14.解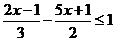 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.
15.设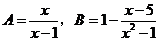 ,当
,当 为何值时,
为何值时,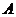 与
与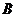 的值相等?
的值相等?
16.先化简,再求值: ,其中,
,其中,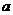 是方程
是方程 的根.
的根.
四、解答题(共2个小题,17小题5分,18小题6分,共11分)
17.如图,E、F是菱形ABCD的对角线BD所在直线上两点,且DE=BF.
请你以F为一个端点,和图中已标有字母的某一点连成一条新的线段,猜想并证明它和已有的某一条线段相等.

(1)连结 ;
(2)猜想: ;
(3)证明:
18.为了保护野生动物,某中学在全校所有学生中,对四种国家一级保护动物的喜爱情况进行问卷调查.要求每位学生只选一种自己最喜爱的动物,调查结果绘制成如下未完整的统计表和统计图,请你根据图表中提供的信息,解答以下问题:
动物名称
频数(学生人数)
频率
金丝猴
0.20
大熊猫
1000
0.50
藏羚羊
500
丹顶鹤
100
0.05
合计
1
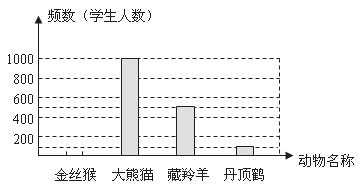
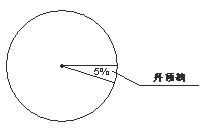
(1)请把表格和统计图分别补充完整;
(2)为了更好地保护野生动物,请你提出一条合理的建议.
19.已知关于x的方程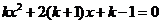 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;(2)请选取一个你喜欢的k值,代入方程并求出方程的根.
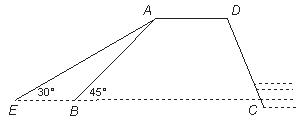
20.一座建于若干年前的水库大坝的横断面为梯形ABCD,如图所示,其中背水面为AB,现准备对大坝背水面进行整修,将坡角由45°改为30°,若测量得AB=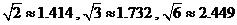 )
)
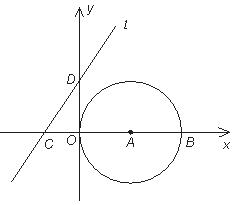
21.如图,在平面直角坐标系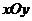 中,以点
中,以点 为圆心的圆与x轴交于原点O和点B,直线l与x轴、y轴分别交于点C(-2,0)、D(0,3).
为圆心的圆与x轴交于原点O和点B,直线l与x轴、y轴分别交于点C(-2,0)、D(0,3).
(1)求出直线l的解析式;
(2)若直线l绕点C顺时针旋转,设旋转后的直线与y轴交于点E(0,b),且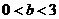 ,在旋转的过程中,直线CE与⊙A有几种位置关系?试求出每种位置关系时,b的取值范围.
,在旋转的过程中,直线CE与⊙A有几种位置关系?试求出每种位置关系时,b的取值范围.
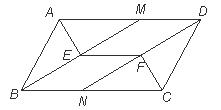
22.已知:如图,平行四边形ABCD中, AE、BE、CF、DF分别平分∠BAD、∠ABC、∠BCD、∠CDA,BE、DF的延长线分别交AD、BC于点M、N,连结EF,若AD=7,AB=4,求EF的长.
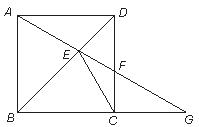
23.已知:如图,在正方形ABCD中,点G是BC延长线一点,连结AG,分别交BD、CD于点E、F.
(1)求证: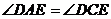 ;
;
(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.
(3)在(2)的条件下,求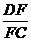 的值.
的值.
24.某校开展“迎2008年北京奥运会”的主题校会活动,老师派小明同学去学校附近的超市购买笔记本作为奖品.小明选择了该超市单价为8元和4.8元的两种笔记本,他要购买这两种笔记本共40本.
(1)如果他一共带了240元,全部用于购买奖品,那么能买这两种笔记本各多少本?
(2)小明根据主题校会活动的设奖情况,决定所购买单价为8元笔记本的数量要少于单价为4.8元笔记本数量的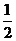 ,但又不少于单价为4.8元笔记本数量的
,但又不少于单价为4.8元笔记本数量的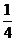 .如果他买了单价为8元的笔记本
.如果他买了单价为8元的笔记本 本,买这两种笔记本共花了
本,买这两种笔记本共花了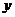 元.①请写出
元.①请写出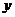 (元)关于
(元)关于 (本)的函数关系式,并求出自变量
(本)的函数关系式,并求出自变量 的取值范围;
的取值范围;
②请帮小明计算一下,这两种笔记本各购买多少本时,所花的钱最少,此时花了多少元钱?
25.在平面直角坐标系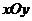 中,抛物线
中,抛物线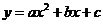 经过A(3,0)、B(5,0)、
经过A(3,0)、B(5,0)、
C(0,5)三点.
(1)求此抛物线的解析式;
(2)设抛物线的顶点为D,求△BCD的面积;
(3)若在抛物线的对称轴上有一个动点P,当△OCP是腰长为5的等腰三角形时,求点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com