
2007-2008学年度北京市宣武区第二学期九年级第一次质量检测
数学试卷
一、选择题(本大题共8小题,每小题4分,共32分,在每小题给出的四个选项中,只有一项是符合题意的)
1.5的算术平方根是
A.25 B.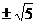 C.
C.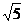 D.
D.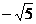
2.如图,已知AB∥CD,AD与BC相交与点P,AB=4,CD=7,PD=10,则AP的长等于

A.40/11
B.70/
3.如图,以Rt△ABC的直角边AC所在的直线为轴,将△ABC旋转一周,所形成的几何体的俯视图是

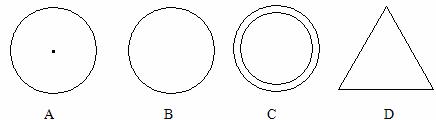
4.⊙O的半径r=
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.可能在⊙O内可能在⊙O外
5.如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是

A.1/8 B.1/
6. 已知一次函数y=kx+b(k,b都是常数,且k≠0),x与y的部分对应值如表所示,那么m的值等于

A.-1 B
7.对于实数a, b, c, d规定一种运算: ,如
,如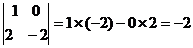 ,那么
,那么 时,x=( )
时,x=( )
A. B.
B.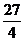 C.
C.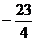 D.
D.
8.如图,边长为1和2的两个正方形的一边在同一水平线上,小正方形沿水平线自左向右匀速穿过大正方行,下图反映了这个运动的全过程。设小正方形的运动时间为t,两正方形重叠部分面积为S,则S与t的函数图像大致为

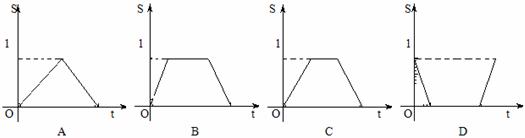
二、填空题(本大题共4小题,每小题4分,共16分,把答案写在题中横线上)
9.如图,是甲乙两地5月下旬的日平均气温统计图,则甲乙两地这10天日平均气温的方差大小关系为:

10.如图,在△ABC中,∠C=90°,AB=

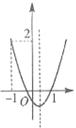
11.如图,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0),且与y
轴相交于负半轴,给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0.其中正确的序号是_____
12.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有一组数:1,1,2,3,4,
8,13,…。其中从第三个数起,每一个数都等于它前面两个数的和。现以这组数中的各个
数作为正方形的边长构造如图所示的正方形:
三、解答题(本大题共13小题,共72分,解答应写出文字说明或演算步骤)
13.(本小题满分5分)现给出三个多项式:x2/2+x-1,x2/2+3x+1,x2/2-x。请你选择其中两个进行加法运算,并把结果因式分解。
14.(本小题满分5分)解方程: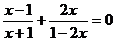
15. (本小题满分5分)解不等式组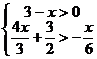 ,并把解集在数轴上表示出来。
,并把解集在数轴上表示出来。
16.(本小题满分5分)m为何正整数时,关于x的一元二次方程x2+4x+m-1=0有两个不相等的实数根。
17.(本小题满分4分)已知△ABC中,∠A=90°,∠B=67.5°。请画一条直线,把这个三角新分割成两个等腰三角形。(请你利用下面给出的备用图,画出两种不同的分割方法。只需要画图,不必说明理由,但要在图中标出相等两角的度数)

18.(本小题满分6分)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径。下图是水平放置的破裂管道有水部分的截面。

(1)作图题:请你用圆规、直尺补全这个输水管道的圆形截面;(不写作法,但要保留作图痕迹)
(2)若这个输水管道有水部分的水面宽AB=
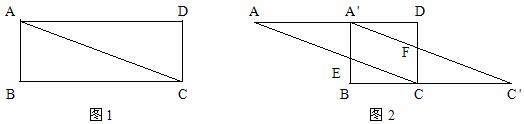
19.(本小题满分6分)将图1中矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图2中的△A’B’C’,除△ADC与△C’BA’全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明。
20.(本小题满分5分)如图,反比例函数y=k/x的图像与一次函数y=mx+b的图像交于A(1,3)、B(n,-1)两点

(1)求反比例函数与一次函数的解析式;
(2)根据图像回答:当x取何值时,此反比例函数的值大于一次函数的值?
21.(本小题满分5分)“农民也可以报销医疗费了!”这是某市推行新型农村合作医疗的成果。村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可以得到按一定比例返回的返回款。这一举措极大地增强了农民抵御大病风险的能力,小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了如下的统计图。

根据以上信息,解答以下问题:
(1)本次调查了多少村民?被调查的村民中。有多少人参加合作医疗得到了返回款?
(2)该乡若有10000名村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年增长率相同,求这个年增长率。
22.(本小题满分5分)如图,在梯形ABCD中,AD∥BC,AD的长为4,S梯形ABCD=9.已知点A、B的坐标分别为(1,0)和(2,-3)

(1)求点C的坐标;
(2)取点E(2,-1),联结DE并延长交AB于F,试猜想DF与AB之间的位置关系,并证明你的结论;
(3)将梯形ABCD绕点A旋转180°后成梯形AB’C’D’,画出梯形AB’C’D’。
23.(本小题满分7分)如图,正方形ABCD边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,且AH=2, 联结CF。

(1)当DG=2时,试求菱形EFGH的边长与△FCG的面积;
(2)设DG=X,试用含x的代数式表示△FCG的面积;
(3)请判断△FCG的面积能否等于1,并说明理由。
24.(本小题满分7分)已知:直线y=x+6交x轴,y轴于A,C两点,经过A,O两点的抛物线y=ax2+bx(a<0)的顶点B在直线AC上。
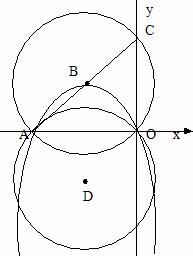
(1)求A,C两点的坐标;
(2)求出该抛物线的函数关系式;
(3)以B为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D。试判断直线AC与⊙D的位置关系
(4)若E为⊙B优弧ACO上一动点,联结AE/OE,问在抛物线上是否存在一点M,使∠MOA:∠AEO=2:3,若存在,试求点M的坐标;若不存在,试说明理由。
25.(本小题满分7分)在坐标平面上,点P从点M( ,1)出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长OA:OB=1:
,1)出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长OA:OB=1: ;过点O且垂直于射线OM的直线l与点P同时出发,且与点P沿相同的方向,以相同的速度运动。
;过点O且垂直于射线OM的直线l与点P同时出发,且与点P沿相同的方向,以相同的速度运动。

(1)在点P运动过程中,试判断AB与y轴的位置关系,并说明理由;
(2)设点P与直线l都运动了t秒,求此时的矩形OAPB与直线l在运动过程中所扫过区域的重叠部分的面积S(用含t的代数式表示)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com