
2009年四川省乐山市高中阶段教育学校招生考试
数学试卷
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求.
1.下列各数中,最小的是( )
A. B.
B.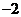 C.
C.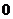 D.
D.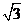
2.温家宝总理在2009年的《政府工作报告》中指出:为应对国际金融危机,实施总额4万亿元的投资计划,刺激经济增长,4万亿元用科学计数法表示为( )
A.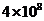 元 B.
元 B.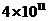 元 C.
元 C.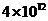 元 D.
元 D.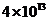 元
元
3.如图,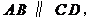
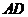 和
和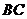 相交于点
相交于点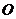 ,
,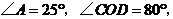 则
则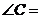 ( )
( )
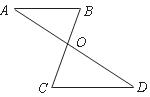
A.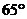 B.
B.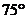 C.
C.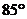 D.
D.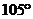
4.下列命题中,假命题是( )
A.两点之间,线段最短
B.角平分线上的点到这个角的两边的距离相等
C.两组对边分别平行的四边形是平行四边形
D.对角线相等的四边形是矩形
5.如果实数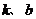 满足
满足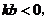 且不等式
且不等式 的解集是
的解集是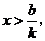 那么函数
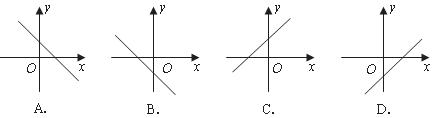
那么函数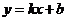 的图象只可能是( )
的图象只可能是( )
6.为了解初三学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的情况,并把它绘制成折线统计图(如图所示).那么关于该班45名同学一周参加体育锻炼时间的说法错误的是( )
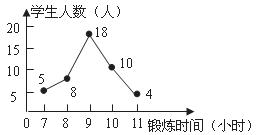
A.众数是9 B.中位数是9
C.平均数是9 D.锻炼时间不低于9小时的有14人
7.在中央电视台2套“开心辞典”节目中,有一期的某道题目是:如图所示,天平中放有苹果、香蕉、砝码,且两个天平都平衡,则一个苹果的重量是一个香蕉的重量的( )
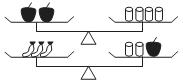
A.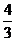 倍
B.
倍
B.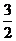 倍 C.
倍 C.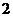 倍
D.
倍
D. 倍
倍
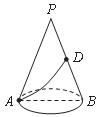
8.如图,一圆锥的底面半径为2,母线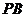 的长为6,
的长为6,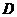 为
为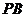 的中点.一只蚂蚁从点
的中点.一只蚂蚁从点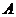 出发,沿着圆锥的侧面爬行到点
出发,沿着圆锥的侧面爬行到点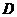 ,则蚂蚁爬行的最短路程为(
)
,则蚂蚁爬行的最短路程为(
)
A.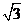 B.
B.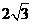 C.
C. D.
D.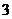
9.已知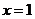 是关于
是关于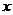 的方程
的方程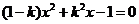 的根,则常数
的根,则常数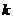 的值为( )
的值为( )
A.0 B.
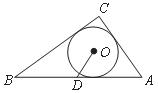
10.如图,在 中,
中,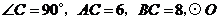 为
为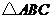 的内切圆,点
的内切圆,点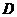 是斜边
是斜边 的中点,则
的中点,则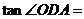 ( )
( )
A.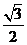 B.
B.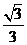 C.
C.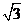 D.2
D.2
第Ⅱ卷(非选择题 共120分)
二、填空题:本大题共6小题,每小题3分,共18分.把答案填在题中的横线上.
11.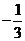 的相反数是
.
的相反数是
.
12.分解因式: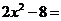 .
.
13.若实数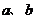 在数轴上对应的点的位置如图所示,则化简
在数轴上对应的点的位置如图所示,则化简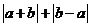 的结果是 .
的结果是 .
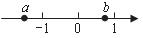
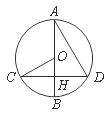
14.如图, 为
为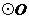 的直径,弦
的直径,弦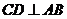 于点
于点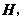 连结
连结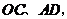 若
若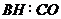
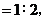
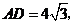 则
则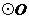 的周长等于
.
的周长等于
.
15.已知正比例函数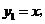 反比例函数
反比例函数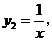 由
由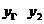 构造一个新函数
构造一个新函数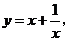 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
①该函数的图象是中心对称图形;
②当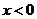 时,该函数在
时,该函数在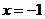 时取得最大值-2;
时取得最大值-2;
③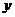 的值不可能为1;
的值不可能为1;
④在每个象限内,函数值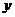 随自变量
随自变量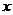 的增大而增大.
的增大而增大.
其中正确的命题是 .(请写出所有正确的命题的序号)
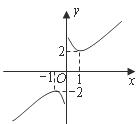
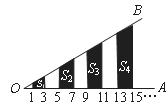
16.如图,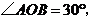 过
过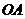 上到点
上到点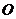 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作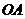 的垂线,分别与
的垂线,分别与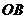 相交,得到如图所示的阴影梯形,它们的面积依次记为
相交,得到如图所示的阴影梯形,它们的面积依次记为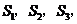 ….则
….则
(1)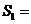 ;
;
(2)通过计算可得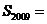 .
.
三、本大题共3小题,每小题9分,共27分.
17.解不等式组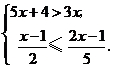
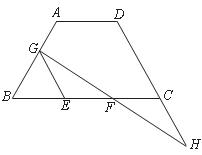
18.如图,在等腰梯形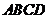 中,
中,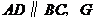 是边
是边 上的一点,过点
上的一点,过点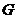 作
作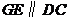 交
交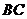 边于点
边于点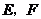 是
是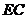 的中点,连结
的中点,连结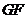 并延长交
并延长交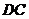 的延长线于点
的延长线于点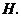 求证:
求证: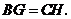
19.若实数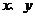 满足
满足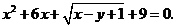 求代数式
求代数式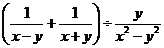 的值.(要求对代数式先化简,再求值.)
的值.(要求对代数式先化简,再求值.)
四、本大题共3小题,每小题10分,共30分.
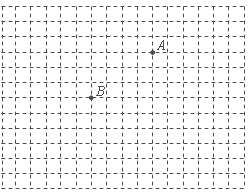
20.下图是由边长为1的小正方形组成的方格图.
(1)请在方格图中建立平面直角坐标系,使点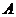 的坐标为
的坐标为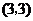 ,点
,点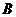 的坐标为
的坐标为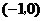 ;
;
(2)在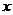 轴上画点
轴上画点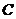 ,使
,使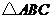 是以
是以 为腰的等腰三角形,并写出所有满足条件的点
为腰的等腰三角形,并写出所有满足条件的点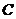 的坐标.(不写作法,保留作图痕迹)
的坐标.(不写作法,保留作图痕迹)
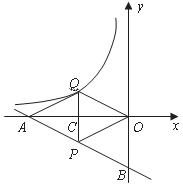
21.如图,一次函数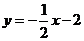 的图象分别交
的图象分别交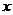 轴、
轴、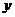 轴于
轴于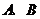 两点,
两点,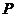 为
为 的中点,
的中点,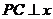 轴于点
轴于点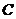 ,延长
,延长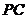 交反比例函数
交反比例函数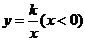 的图象于点
的图象于点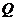 ,且
,且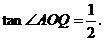
(1)求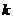 的值;
的值;
(2)连结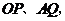 求证:四边形
求证:四边形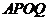 是菱形.
是菱形.
22.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个.若从中任意摸出一个球,这个球是白球的概率为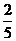 .
.
(1)求口袋中红球的个数;
(2)把口袋中的球搅匀后摸出一个球,放回搅匀再摸出第二个球,求摸到的两个球是一红一白的概率.(请结合树状图或列表加以解答)
五、本大题共2小题,每小题10分,共20分.
23.本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分。
甲题:关于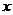 的一元二次方程
的一元二次方程 有两个不相等的实数根
有两个不相等的实数根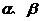 .
.
(1)求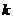 的取值范围;
的取值范围;
(2)若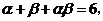 求
求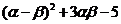 的值.
的值.
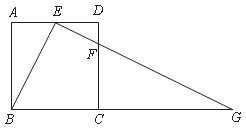
乙题:如图(13),在正方形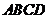 中,
中,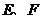 分别是边
分别是边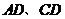 上的点,
上的点,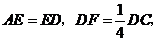 连结
连结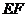 并延长交
并延长交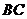 的延长线于点
的延长线于点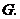
(1)求证: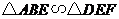 ;
;
(2)若正方形的边长为4,求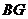 的长.我选做的是___________.
的长.我选做的是___________.
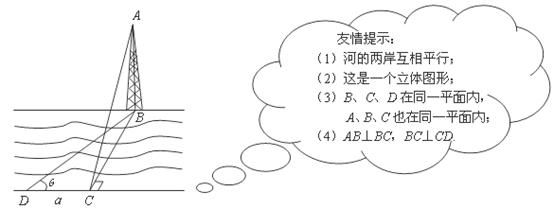
24.如图,某学习小组为了测量河对岸塔 的高度,在塔底部点
的高度,在塔底部点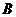 的正对岸点
的正对岸点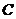 处,测得塔顶点
处,测得塔顶点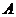 的仰角为
的仰角为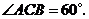
(1)若河宽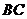 是
是 的高度;(结果精确到
的高度;(结果精确到
(2)若河宽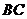 的长度不易测量,如何测量塔
的长度不易测量,如何测量塔 的高度呢?小强思考了一种方法:从点
的高度呢?小强思考了一种方法:从点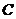 出发,沿河岸前行
出发,沿河岸前行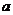 米至点
米至点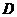 处,若在点
处,若在点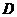 处测出
处测出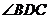 的度数
的度数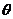 ,这样就可以求出塔
,这样就可以求出塔 的高度了.
的高度了.
小强的方法可行吗?若行,请用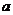 和
和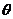 表示塔
表示塔 的高度,若不能,请说明理由.
的高度,若不能,请说明理由.
六、本大题共2小题,第25题12分,第26题13分,共计25分.
25.如图,在梯形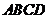 中,
中, 厘米,
厘米,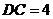 厘米,
厘米,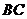 的坡度
的坡度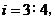 动点
动点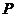 从
从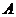 出发以2厘米/秒的速度沿
出发以2厘米/秒的速度沿 方向向点
方向向点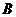 运动,动点
运动,动点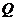 从点
从点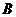 出发以3厘米/秒的速度沿
出发以3厘米/秒的速度沿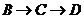 方向向点
方向向点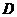 运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为
运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为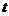 秒.
秒.
(1)求边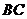 的长;
的长;
(2)当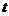 为何值时,
为何值时,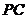 与
与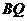 相互平分;
相互平分;
(3)连结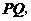 设
设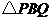 的面积为
的面积为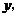 探求
探求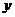 与
与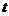 的函数关系式,求
的函数关系式,求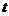 为何值时,
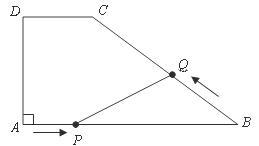
为何值时,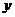 有最大值?最大值是多少?
有最大值?最大值是多少?
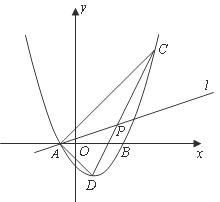
26.如图,在平面直角坐标系中,开口向上的抛物线与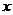 轴交于
轴交于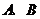 两点,
两点,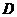 为抛物线的顶点,
为抛物线的顶点,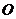 为坐标原点.若
为坐标原点.若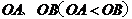 的长分别是方程
的长分别是方程 的两根,且
的两根,且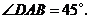
(1)求抛物线对应的二次函数解析式;
(2)过点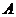 作
作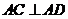 交抛物线于点
交抛物线于点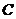 ,求点
,求点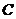 的坐标;
的坐标;
(3)在(2)的条件下,过点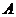 任作直线
任作直线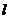 交线段
交线段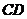 于点
于点 求
求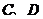 到直线
到直线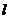 的距离分别为
的距离分别为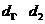 ,试求
,试求 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com