
2008-2009学年度德州市禹城第二学期八年级期末教学质量检测
数学试题
(满分120分 考试时间120分钟)
一、选择题(每个小题3分,共24分)
1.分式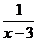 专有意义,则
专有意义,则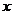 的取值范围是( )
的取值范围是( )
A.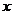 >3 B.
>3 B.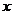 <
<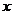 ≠3 D.
≠3 D.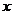 ≠-3
≠-3
2.分式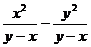 的结果是( )
的结果是( )
A.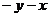 B.
B.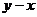 C.
C.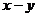 D.
D.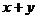
3.四边形ABCD,仅从下列条件中任取两个加以组合,使得四边形ABCD是平行四边形,一共有多少种不同的组合?( )
①AB//CD;②BC//AD;③AB=CD;④BC=AD
A.2组 B.3组 C.4组 D.6组
4.某品牌服装销售商对各种型号服装的市场占有率进行调查时,他最应该关注的是服装型号的( )
A.平均数 B.众数 C.中位数 D.极差
5.正比例函数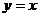 与反比例函数
与反比例函数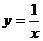 的图象相交于点A、C,AB⊥
的图象相交于点A、C,AB⊥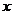 轴于B,CD⊥
轴于B,CD⊥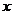 轴于D,则四边形ABCD的面积为( )
轴于D,则四边形ABCD的面积为( )
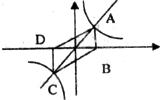
A.1 B.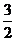 D.
D.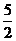
6.如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠B=60°,BC=3,△ABE的周长为6。则等腰梯形ABCD的周长是( )
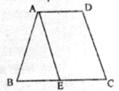
A.8 B.
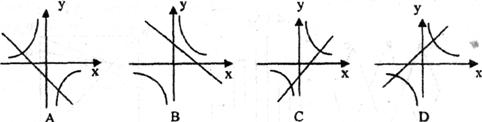
7.如图,在同一直角坐标系中,一次函数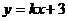 与反比例函数
与反比例函数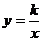 的图象位置可能是( )
的图象位置可能是( )
8.如图.已知矩形ABCD,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当P在BC上从B向C移动,而R不动时,那么下列结论成立的是( )
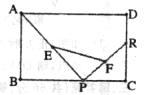
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不改变 D.线段EF的长不能确定
二、填空题(每题3分,共30分)
9.分式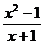 的值为0,则
的值为0,则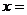 _____________.
_____________.
10.化简 ____________.
____________.
11.已知反比侧函数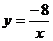 的图象经过点P(
的图象经过点P(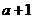 ,4),则
,4),则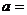 __________.
__________.
12.已知点A(-2,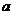 ),B(-l,b),C(3,c)在双曲线
),B(-l,b),C(3,c)在双曲线 上,则
上,则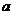 、b、c的大小关系为_________________.(用“<”连接)
、b、c的大小关系为_________________.(用“<”连接)
13.已知一组数据9,9,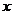 ,7的平均数与众数恰好相等,则这组数据的中位数是________________.
,7的平均数与众数恰好相等,则这组数据的中位数是________________.
14.已知,等腰梯形ABCD中,AD//BC,对角线AC⊥BD,AD=
15.在四边形ABCD中,AB∥CD,若加上AD∥BC,则四边形ABCD为平行四边形.现在请你添加一个适当的条件:_________________________________,使得四边形AECF为平行四边形.(图中不再添加点和线)
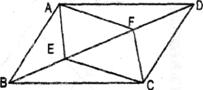
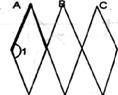
16.如图,是根据四边形的不稳定性制作的边长为
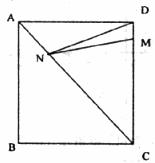
18.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是对角线AC上一个动点,则DM+DN的最小值为___________.
三、解答题(共66分)解答时请写出必要的演算过程或推理步骤。
19.(本小题6分)
先化简并求值: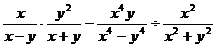 .其中
.其中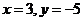 .
.
20.(本小题6分)
解方程: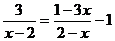 .
.
21.(本题8分)
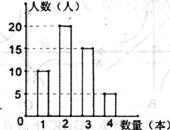
张老师要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”.为此,他对两位同学进行了辅导。并在辅导期间测验了10次,测验成绩如下表:
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
第9次
第10次
甲
68
80
78
79
78
84
81
83
77
92
乙
86
80
75
83
79
80
85
80
77
75
利用表中数据,解答下列问题:
(1)填空完成下表:
平均成绩
中位数
众数
甲
79.5
乙
80
(2)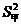 =33.2,请你计算乙10次测验成绩的方差.
=33.2,请你计算乙10次测验成绩的方差.
(3)请你根据上面的信息,运用所学统计知识,帮
22.(本小题8分)
已知:如图,点D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE.
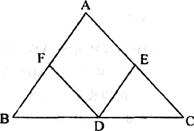
求证:(1)△ABC是等腰三角形;
(2)当∠A=90°时,试判断四边形AFDE是怎样酶四边形.证明你的判断结论.
23.(本小题7分)
2008年初我国南方发生雪灾,某地电线被雪压断,供电局的维修队要到30千米远的郊区进行抢修,维修工骑摩托车先走,15分钟后,抢修车装载所需材料出发,结果两车同时到达抢修点.已知抢修车的速度是摩托车速度的1.5倍,求两种车的速度.
24.(本小题10分)
如图,Rt△ABO的顶点A是双曲线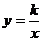 与直线
与直线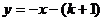 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥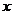 轴于B,且S△ABO=
轴于B,且S△ABO=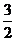 。直线
。直线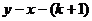 与
与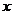 轴交点是D.
轴交点是D.
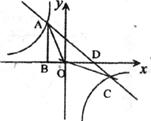
(1)求这两个函数解析式;
(2)若两个函数的交点的坐标为A(-1,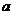 ),C(b,-l)时,求△AOC的面积.
),C(b,-l)时,求△AOC的面积.
25.(本小题10分)
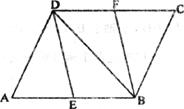
如图,在□ABCD中,E、F分别为边AB、CD的中点.连接DE、BF,BD.
(1)求证:△ADEC≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊的四边形?证明你的结论.
26.(本小题11分)
已知:如图,在△ABC中,AB=AC,若将△ABC绕点C腰时针旋转180°后,得到△FEC.
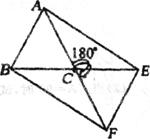
(1)试猜想线段AE与BF有何数量关系?说明理由.
(2)若△ABC的面积为
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com