2,4,6 本卷包括必考题和选考题两部分.第11题到第20题为必考题,每个试题考生都必须作答;第21题为选考题,请考生根据要求选答.
试题详情
二、填空题(本大题共5小题,每小题4分,共20分,把你的答案填在答题卷相应题号的横线上) 11.已知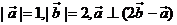 ,则 ,则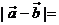 ____________. ____________. 试题详情
试题详情
试题详情
 14.古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有
种(结果用数值表示). 14.古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有
种(结果用数值表示).
试题详情
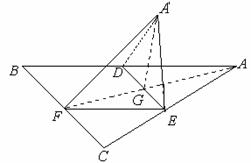
15.如图所示,正△ABC的中线AF与中位线DE相
交于点G,已知△A/ED是△AED绕边DE旋转过程中的一个图形,现给出下列四个命题:
1动点A/在平面ABC上的射影在线段AF上;
2恒有平面A/GF⊥平面BCED;
3三棱锥A/-FED的体积有最大值;
4异面直线A/E与BD不可能垂直.
其中正确命题的序号是
.(写出所有正确命题的序号) 试题详情
三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤) 16. (本小题满分13分)设函数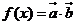 ,其中向量 ,其中向量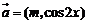 , , 试题详情
试题详情
(1)求实数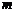 的值;(2)求函数 的值;(2)求函数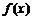 的最小值及此时 的最小值及此时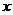 值的集合. 值的集合. 试题详情
试题详情
(I)证明平面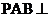 平面ABC; 平面ABC; (Ⅱ)求直线PB与平面PAC所成角的正弦值。 试题详情
18. (本小题满分13分)为应对金融危机,刺激消费,某市给市民发放面额为100元的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表: 试题详情
200元 300元 400元 500元 老年 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
0.2 某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点, (1) 求这三人恰有两人消费额大于300元的概率; (2) 求这三人消费总额大于或等于1300元的概率; 试题详情
(3) 设这三人中消费额大于300元的人数为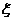 ,求 ,求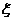 的分布列及 的分布列及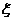 的数学期望。 的数学期望。 试题详情
试题详情
(Ⅰ)当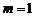 时,求椭圆的方程; 时,求椭圆的方程; 试题详情
试题详情
(Ⅲ)是否存在实数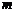 ,使得 ,使得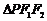 的边长是连续的自然数,若存在,求出这样的实数 的边长是连续的自然数,若存在,求出这样的实数 ;若不存在,请说明理由. ;若不存在,请说明理由. 试题详情
20.(本题满分14分)函数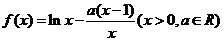 . . 试题详情
(1)试求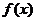 的单调区间; 的单调区间; 试题详情
试题详情
(3)求证:不等式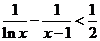 对于 对于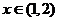 恒成立. 恒成立. 试题详情
21.选考题(本题满分14分,共3小题,任选其中2题作答,每小题7分) (Ⅰ)选修4―2:矩阵与变换: 试题详情
试题详情
试题详情
试题详情
一、ABCBD BCABD 二、11.2 12.  13.4 14.10 15. ①②③ 13.4 14.10 15. ①②③ 三、16. 解:(1) ,
3分 ,
3分 由已知 ,得 ,得 .
6分 .
6分 (2)由(1)得 ,
8分 ,
8分  当 当 时, 时, 的最小值为 的最小值为 ,
10分 ,
10分
由 ,得 ,得 值的集合为 值的集合为 . 13分 . 13分 17. 解:(I)取AB的中点O,连接OP,OC  PA=PB PA=PB  PO PO AB AB 又在 中, 中, , , 在 中, 中, ,又 ,又 ,故有 ,故有  又 又 , ,  面ABC 4分 面ABC 4分 又 PO 面PAB, 面PAB, 面PAB 面PAB 面ABC
6分 面ABC
6分 (Ⅱ)以O为坐标原点,
分别以OB,OC,OP为 轴, 轴, 轴, 轴, 轴建立坐标系, 轴建立坐标系,  如图,则A 如图,则A 8分 8分
  设平面PAC的一个法向量为 。 。  得 得 令 ,则 ,则  11分
11分 设直线PB与平面PAC所成角为 , , 于是 13分
13分 18. 解:(1) ;
4分 ;
4分 (2)消费总额为1500元的概率是: 5分
5分 消费总额为1400元的概率是: 6分 6分 消费总额为1300元的概率是:  = = , ,
所以消费总额大于或等于1300元的概率是 ;
8分 ;
8分 (3) , ,  , ,
 = =
 。所以 。所以 的分布列为: 的分布列为:

0 1 2 3 
0.294 0.448 0.222 0.036 数学期望是: 。 13分 。 13分 19. 解:∵ 的右焦点 的右焦点  ∴椭圆的半焦距 ∴椭圆的半焦距 ,又 ,又 , ,
∴椭圆的 , ,  .椭圆方程为 .椭圆方程为 . . (Ⅰ)当 时,故椭圆方程为 时,故椭圆方程为 , 3分 , 3分 (Ⅱ)依题意设直线 的方程为: 的方程为: , , 联立 得点 得点 的坐标为 的坐标为 . 4分 . 4分 将 代入 代入 得 得 . . 设 、 、 ,由韦达定理得 ,由韦达定理得 , , . 5分 . 5分 又 , , . . 
 7分 7分  有实根, ∴点 有实根, ∴点 可以在圆上. 8分 可以在圆上. 8分
(Ⅲ)假设存在满足条件的实数 , , 由 解得: 解得: . 10分 . 10分 ∴ , , ,又 ,又 .即 .即 的边长分别是 的边长分别是 、 、 、 、 . .  时,能使 时,能使 的边长是连续的自然数。 1 的边长是连续的自然数。 1 3分 3分 20. 解:(1) .
1分 .
1分 当 时, 时, , , 在 在 上单调递增;
2分 上单调递增;
2分 当 , , 时, 时, , , 在 在 上单调递减; 上单调递减;  时, 时, , , 在 在 上单调递增.
3分 上单调递增.
3分
综上所述,当 时, 时, 的单调递增区间为 的单调递增区间为 ;当 ;当 时, 时, 的单调递增区间为 的单调递增区间为 ,单调递减区间为 ,单调递减区间为 .
4分 .
4分 (2)充分性: 时,由(1)知, 时,由(1)知, 在x=1处有极小值也是最小值, 在x=1处有极小值也是最小值, 即 。而 。而 在 在 上单调递减,在 上单调递减,在 上单调递增, 上单调递增, 所以 在 在 上有唯一的一个零点x=1. 6分 上有唯一的一个零点x=1. 6分 必要性:若函数f(x)存在唯一零点,即方程 =0在 =0在 上有唯一解, 上有唯一解, 因 , 由(1)知, , 由(1)知, 在 在 处有极小值也是最小值f(a), 处有极小值也是最小值f(a),  f(a)=0,即 f(a)=0,即 .
7分 .
7分
令 , ,  . . 当 时, 时, , , 在上单调递增;当 在上单调递增;当 时, 时, , ,  在 在 上单调递减。 上单调递减。  , , =0只有唯一解 =0只有唯一解 . .
因此 =0在 =0在 上有唯一解时必有 上有唯一解时必有 . . 综上:在 时, 时,  =0在 =0在 上有唯一解的充要条件是 上有唯一解的充要条件是 . 9分 . 9分 (3)证明:∵1<x<2, ∴ . . 令 ,∴ ,∴  ,11分 ,11分 由(1)知,当 时, 时, ,∴ ,∴ , , ∴ .∴ .∴ ,
12分 ,
12分 ∴F(x)在(1,2)上单调递增,∴ , , ∴ 。∴ 。∴ .
14分 .
14分 21. (Ⅰ)解:考虑在矩阵 作用下,求出变换后的三角形的顶点坐标,从而求得三角形的面积,可先求得 作用下,求出变换后的三角形的顶点坐标,从而求得三角形的面积,可先求得 ,由 ,由  = = ,得点 ,得点 在矩阵 在矩阵 作用下变换所得到的点 作用下变换所得到的点 ,同理求得 ,同理求得 在矩阵 在矩阵 作用下变换所得到的点分别是 作用下变换所得到的点分别是 , , ,计算得△ ,计算得△ 的面积为3.
7分 的面积为3.
7分 (Ⅱ)解:直线 的极坐标方程 的极坐标方程 ,则 ,则 , , 即 ,所以直线 ,所以直线 的直角坐标方程为 的直角坐标方程为 ; 2分 ; 2分 设 ,其中 ,其中 ,则P到直线 ,则P到直线 的距离 的距离  ,其中 ,其中 ,∴ 当 ,∴ 当 时, 时, 的最大值为 的最大值为 ;当 ;当 时, 时, 的最小值为 的最小值为 。
7分 。
7分
(Ⅲ)解:由柯西不等式,得 , 2分 , 2分 即 .由条件,得 .由条件,得 .解得 .解得 , 2分 , 2分 当且仅当 时等号成立.代入 时等号成立.代入 时, 时, ; ; 时, 时, .所以, .所以, 的取值范围是 的取值范围是 .
7分 .
7分
| 
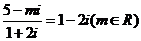 ,则
,则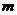 的值为
( )
的值为
( )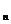 }中,已知a
}中,已知a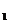 =2,a
=2,a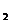 +a
+a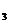 =13,则a
=13,则a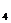 +a
+a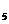 +a
+a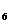 等于( )
等于( )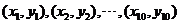 满足线性回归方程
满足线性回归方程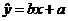 ,则“
,则“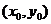 满足线性回归方程
满足线性回归方程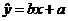 ”是“
”是“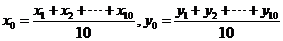 ”的 ( )
”的 ( )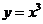 与
与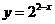 的图象的交点为
的图象的交点为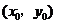 ,则
,则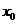 所在的区间是 ( )
所在的区间是 ( )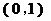 B.
B.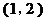 C.
C.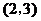 D.
D.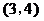
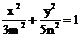 和双曲线
和双曲线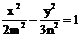 有公共的焦点,那么双曲线的渐近线方程为( )
有公共的焦点,那么双曲线的渐近线方程为( )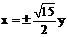 B.
B. 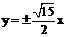 C.
C. 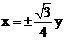 D.
D. 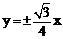
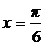 是函数
是函数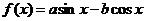 图象的一条对称轴,则函数
图象的一条对称轴,则函数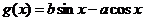 图象的一条对称轴方程是 ( )
图象的一条对称轴方程是 ( )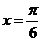 B.
B.
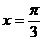 C.
C.
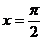 D.
D.
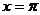
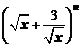 展开式中,各项系数的和与其各项二项式系数的和之比为64,则展开式中的常数项等于 (
)
展开式中,各项系数的和与其各项二项式系数的和之比为64,则展开式中的常数项等于 (
)
 8. 已知命题
8. 已知命题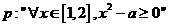 ,命题
,命题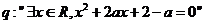 ,若命题“
,若命题“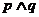 ” 是真命题,则实数
” 是真命题,则实数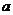 的取值范围是 ( )
的取值范围是 ( )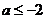 或
或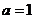 B.
B. 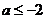 或
或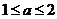 C.
C. 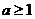 D.
D. 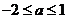
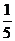 B.0 C.
B.0 C.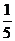 D.5
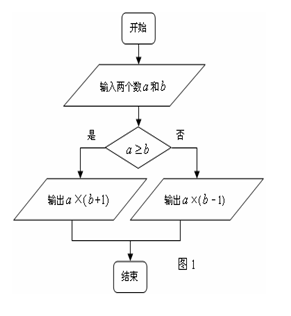
D.5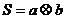 ,运算原理如图1所示,则式子:
,运算原理如图1所示,则式子: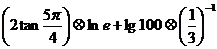 的值是 ( )
的值是 ( ) C.7 D.8
C.7 D.8